【题目】如图,四边形ABCD中,∠B=90°,AB=BC=3 ![]() ,CD=8,AD=10.
,CD=8,AD=10. 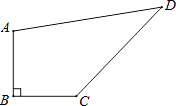
(1)求∠BCD的度数.
(2)求四边形ABCD的面积.
参考答案:
【答案】
(1)解:连接AC,

在Rt△ABC中,∠B=90°,AB=BC=3 ![]() ,
,
根据勾股定理得:AC= ![]() =6,∠ACB=45°,
=6,∠ACB=45°,
∵CD=8,AD=10,
∴AD2=AC2+CD2,
∴△ACD为直角三角形,即∠ACD=90°,
则∠BCD=∠ACB+∠ACD=135°;
(2)解:根据题意得:S四边形ABCD=S△ABC+S△ACD= ![]() ×3
×3 ![]() ×3
×3 ![]() +
+ ![]() ×6×8=9+24=33
×6×8=9+24=33
【解析】(1)连接AC,在直角三角形ABC中,利用勾股定理求出AC的长,再由CD与AD的长,利用勾股定理的逆定理判断得到三角形ACD为直角三角形,再由等腰直角三角形的性质,根据∠BCD=∠ACB+∠ACD即可求出;(2)四边形ABCD面积=三角形ABC面积+三角形ACD面积,求出即可.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对勾股定理的逆定理的理解,了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形ABCD中,∠BAC=90°,AB=AC=1,以AC为一边在△ABC外部作等腰直角三角形ACD,则线段BD的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】沈阳地铁一号线的开通运行给沈阳市民的出行方式带来了一些变化.小王和小林准备利用课余时间,以问卷的方式对沈阳市民的出行方式进行调查.如图是沈阳地铁一号线图(部分),小王和小林分别从太原街站(用A表示)、南市场站(用B表示)、青年大街站(用C表示)这三站中,随机选取一站作为调查的站点.
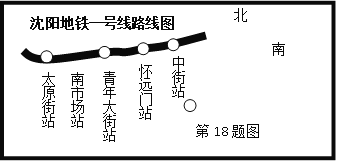
⑴在这三站中,小王选取问卷调查的站点是太原街站的概率是多少?(请直接写出结果)
⑵请你用列表法或画树状图(树形图)法,求小王选取问卷调查的站点与小林选取问卷调查的站点相邻的概率.(各站点用相应的英文字母表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是1800°,这个多边形是边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市展览馆某天四个时间段进出馆人数统计如下表,则馆内人数变化最大的时间段为_______________.
9:00-10:00
10:00-11:00
14:00-15:00
15:00-16:00
进馆人数
50
24
55
32
出馆人数
30
65
28
45
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个十边形所有内角都相等,它的每一个外角等于度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:4m2﹣36= .
相关试题

