【题目】如图,AB是⊙O的直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE交AB于点F,连接DF. 
(1)求证:△DAC≌△ECP;
(2)填空: ①四边形ACED是何种特殊的四边形?
②在点P运动过程中,线段DF、AP的数量关系是 ![]() .
.
参考答案:
【答案】
(1)证明:∵DE为切线,
∴OD⊥DE,
∴∠CDE=90°,
∵点C为AP的中点,
∴DC⊥AP,
∴∠DCA=∠DCP=90°,
∵AB是⊙O直径,
∴∠APB=90°,
∴四边形DEPC为矩形,
∴DC=EP,
在△DAC和△ECP中
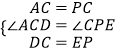 ,
,
∴△DAC≌△ECP;
(2)①∵△DAC≌△ECP,
∴AD=CE,∠DAC=∠ECP,
∴AD∥CE,
∴四边形ACED是平行四边形
②线段DF、AP的数量关系是DF= ![]() AP
AP
【解析】②∵OA=OD, ∴∠DAO=∠ADO,
∵AD∥CE,
∴∠ADO=∠DCF,
∴∠DAO=∠DCF,
∴A,C,F,D四点共圆,
∴ ![]() =
= ![]() ,
,
∴AC=DF,
∵AC= ![]() AP,
AP,
∴DF= ![]() AP,
AP,
所以答案是:DF= ![]() AP.
AP.
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径).
-
科目: 来源: 题型:
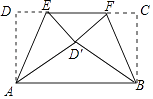
查看答案和解析>>【题目】如图,矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点F为CD上一个动点,把△BCF沿BF折叠,当点D的对应点和点C的对应点都落在点D′处时,EF的长为 .
-
科目: 来源: 题型:
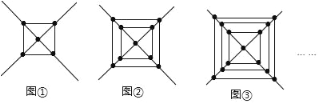
查看答案和解析>>【题目】观察下列各图形中点的个数,根据其中蕴含的规律回答下列问题:
(1)图①中有 个点;图②中有 个点;图③中有 个点;
(2)请用代数式表示出第n个图形中点个数;并求第10个图形中共有多少个点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A坐标为(0,3),点B在x轴上
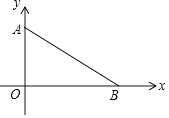
(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若函数y=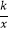 的图象经过点M,且sin∠OAB=
的图象经过点M,且sin∠OAB= 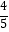 ,求k的值.
,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=20,AC=15,BC边上的高为12,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解,回答下列问题:
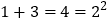
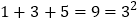
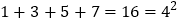
(1)试猜想:1+3+5+7+9+…+2015+2017+2019的和是多少?
(2)推广:1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少?
(3)计算:103+105+107+…+2017+2019.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;

(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
相关试题

