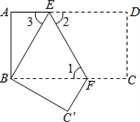
【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)若∠1=60°,求∠3的度数;
(2)求证:BE=BF
(3)若AB=6,AD=12,求△BEF的面积.
参考答案:
【答案】(1)60°;(2)证明见解析;(3)7.5
【解析】试题分析:(1)根据平行线的性质、翻转变换的性质解答;
(2)根据等腰三角形的性质证明;
(3)根据翻转变换的性质、勾股定理计算即可.
试题解析:(1)∵AD∥BC,
∴∠2=∠1=60°,
由翻转变换的性质可知,∠BEF=∠2=60°,
∴∠3=60°;
(2)证明:∵∠BEF=∠1=60°,
∴BE=BF;
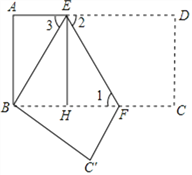
(3)由翻转变换的性质可知,BE=DE=12-AE,
由勾股定理得,BE2=AB2+AE2,即(12-AE)2=62+AE2,
解得,AE=4.5,
则BF=BE=7.5,
∵四边形ABHE是矩形,
∴EH=AB=6,
∴△BEF的面积=![]() ×BF×EH=22.5.
×BF×EH=22.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校需要购买一批篮球和足球,已知一个篮球比一个足球的价格高30元.买两个篮球和三个足球共需510元.
(1)求篮球和足球的单价;
(2)根据需要,学校决定购买篮球和足球共100个,其中篮球的数量不少于足球数量的
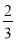 ,用于购买这批篮球和足球的资金不超过10300元,请问有哪几种购买方案?并指出其中费用最低的方案.
,用于购买这批篮球和足球的资金不超过10300元,请问有哪几种购买方案?并指出其中费用最低的方案. -
科目: 来源: 题型:
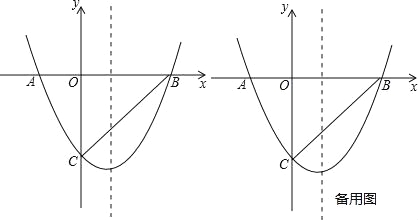
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣2,0)和点B(4,0),与y轴交于点C(0,﹣4).
(1)求二次函数的解析式,并写出抛物线的对称轴,顶点坐标;
(2)设E时抛物线对称轴上一点,当∠BEC=90°时,求点E的坐标;
(3)若P(m,n)是抛物线上一个动点(其中m>0,n<0),是否存在这样的点P,使得△PBC的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(a+2b﹣c)(a﹣b+2c)=[a﹣(_______)][a+(_______)]
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各题中的数是准确数的是( ).
A.初一年级有400名同学
B.月球与地球的距离约为38万千米
C.毛毛身高大约158㎝
D.今天气温估计30℃ -
科目: 来源: 题型:
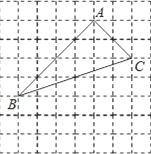
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.
(1)试根据三角形三边关系,判断△ABC的形状;
(2)在方格纸中利用直尺分别画出AB、BC的垂直平分线(要求描出关键格点),交点为O.问点O到△ABC三个顶点的距离相等吗?说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为2,一点P到圆心O的距离为4,则点P在( )
A. 圆内B. 圆上C. 圆外D. 无法确定
相关试题

