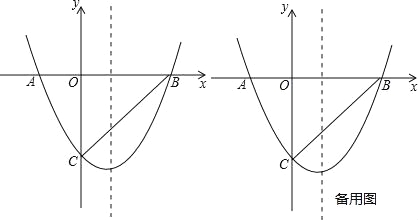
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣2,0)和点B(4,0),与y轴交于点C(0,﹣4).
(1)求二次函数的解析式,并写出抛物线的对称轴,顶点坐标;
(2)设E时抛物线对称轴上一点,当∠BEC=90°时,求点E的坐标;
(3)若P(m,n)是抛物线上一个动点(其中m>0,n<0),是否存在这样的点P,使得△PBC的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)、y=![]() x2﹣x﹣4;对称轴为x=1,顶点坐标为(1,﹣
x2﹣x﹣4;对称轴为x=1,顶点坐标为(1,﹣![]() );(2)、(1,﹣2﹣
);(2)、(1,﹣2﹣![]() )或(1,﹣2+
)或(1,﹣2+![]() );(3)、(2,﹣4),最大值为4.
);(3)、(2,﹣4),最大值为4.
【解析】
试题分析:(1)、由点A、B、C三点的坐标利用待定系数法即可求出二次函数的解析式,再利用配方法将其化成顶点式即可找出该抛物线的对称轴及顶点坐标;(2)、设点E的坐标为(1,t),由两点间的距离公式可求出BE、CE、BC的长,根据勾股定理即可得出关于t的一元二次方程,解方程即可得出点E的坐标;
(3)、由点P在抛物线上,可用m表示出n,由点B、C的坐标利用待定系数法即可求出直线BC的解析式,再由点到直线的距离求出点P到直线BC的距离,根据三角形的面积公式即可得出S△PBC关于m的关系式,利用二次函数的性质即可解决最值问题.
试题解析:(1)、将点A(﹣2,0)、B(4,0)、C(0,﹣4)代入y=ax2+bx+c中,
得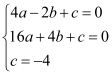 ,解得:
,解得: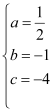 , ∴二次函数的解析式为y=
, ∴二次函数的解析式为y=![]() x2﹣x﹣4.
x2﹣x﹣4.
∵y=![]() x2﹣x﹣4=
x2﹣x﹣4=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() , ∴该抛物线的对称轴为x=1,顶点坐标为(1,﹣
, ∴该抛物线的对称轴为x=1,顶点坐标为(1,﹣![]() ).
).
(2)、依照题意,画出图形,如图1所示. 设点E的坐标为(1,t), ∵B(4,0)、C(0,﹣4),
∴BE=![]() ,CE=
,CE=![]() ,BC=4
,BC=4![]() , ∵∠BEC=90°,∴BE2+CE2=BC2,即9+t2+t2+8t+17=32,
, ∵∠BEC=90°,∴BE2+CE2=BC2,即9+t2+t2+8t+17=32,
解得:t1=﹣2+![]() ,t2=﹣2﹣
,t2=﹣2﹣![]() , 即点E的坐标为(1,﹣2﹣
, 即点E的坐标为(1,﹣2﹣![]() )或(1,﹣2+
)或(1,﹣2+![]() ).
).
(3)、假设存在,如图2所示. ∵P(m,n)是抛物线上一个动点(其中m>0,n<0),
∴n=![]() m2﹣m﹣4,0<m<4. 设直线BC的解析式为y=kx﹣4, ∵点B(4,0)为直线BC上的点,
m2﹣m﹣4,0<m<4. 设直线BC的解析式为y=kx﹣4, ∵点B(4,0)为直线BC上的点,
∴0=4k﹣4,解得:k=1, ∴直线BC的解析式为y=x﹣4,即x﹣y﹣4=0.
点P到直线BC的距离d= =|﹣
=|﹣![]() m2+
m2+![]() m|, ∵0<m<4,
m|, ∵0<m<4,
∴d=﹣![]() m2+
m2+![]() m. S△PBC=
m. S△PBC=![]() BCd=
BCd=![]() ×4
×4![]() ×(﹣
×(﹣![]() m2+
m2+![]() m)=﹣m2+4m=﹣(m﹣2)2+4,
m)=﹣m2+4m=﹣(m﹣2)2+4,
∴当m=2,即点P的坐标为(2,﹣4)时,S△PBC取最大值4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
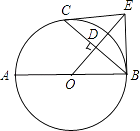
(1)求证:BE与⊙O相切;
(2)连接AD并延长交BE于点F,若OB=9,sin∠ABC= ,求BF的长.
,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法,分别按要求取0.06018的近似值,下列四个结果中错误的是( )。
A.0.1(精确到0.1)
B.0.06(精确到0.001)
C.0.06(精确到0.01)
D.0.0602(精确到0.0001) -
科目: 来源: 题型:
查看答案和解析>>【题目】学校需要购买一批篮球和足球,已知一个篮球比一个足球的价格高30元.买两个篮球和三个足球共需510元.
(1)求篮球和足球的单价;
(2)根据需要,学校决定购买篮球和足球共100个,其中篮球的数量不少于足球数量的
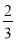 ,用于购买这批篮球和足球的资金不超过10300元,请问有哪几种购买方案?并指出其中费用最低的方案.
,用于购买这批篮球和足球的资金不超过10300元,请问有哪几种购买方案?并指出其中费用最低的方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】(a+2b﹣c)(a﹣b+2c)=[a﹣(_______)][a+(_______)]
-
科目: 来源: 题型:
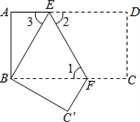
查看答案和解析>>【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)若∠1=60°,求∠3的度数;
(2)求证:BE=BF
(3)若AB=6,AD=12,求△BEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各题中的数是准确数的是( ).
A.初一年级有400名同学
B.月球与地球的距离约为38万千米
C.毛毛身高大约158㎝
D.今天气温估计30℃
相关试题

