【题目】如图1,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
(1)求点D的坐标(用含m的代数式表示);
(2)当△APD是等腰三角形时,求m的值;
(3)设过P、M、B三点的抛物线与x轴正半轴交于点E,过点O作直线ME的垂线,垂足为H(如图2),当点P从点O向点C运动时,点H也随之运动.请直接写出点H所经过的路径长.(不必写解答过程)
参考答案:
【答案】
(1)
解:由题意得CM=BM,
∵∠PMC=∠DMB,
∴Rt△PMC≌Rt△DMB,
∴DB=PC,
∴DB=2﹣m,AD=4﹣m,
∴点D的坐标为(2,4﹣m)
(2)
解:分三种情况
①若AP=AD,则4+m2=(4﹣m)2,解得 ![]() ;
;
②若PD=PA
过P作PF⊥AB于点F(如图),
则AF=FD= ![]() AD=
AD= ![]() (4﹣m)
(4﹣m)
又∵OP=AF,
∴ ![]()
则 ![]()
③若PD=DA,
∵△PMC≌△DMB,
∴PM= ![]() PD=
PD= ![]() AD=
AD= ![]() (4﹣m),
(4﹣m),
∵PC2+CM2=PM2,
∴ ![]() ,
,
解得 ![]() (舍去).
(舍去).
综上所述,当△APD是等腰三角形时,m的值为 ![]() 或
或 ![]() 或
或 ![]()

(3)
解:点H所经过的路径长为 ![]() ;
;
理由是:∵P(0,m)是线段OC上一动点(C点除外),
∴0≤m<2,
当O与P重合时,P点才开始运动,过P、M、B三点的抛物线y=﹣x2+3x,
此时ME的解析式为y=﹣x+3,则∠MEO=45°,
又∵OH⊥EM,
∴△OHE为等腰直角三角形,
∴点O、H、B三点共线,
∴点H所经过的路径以OM为直径的劣弧 ![]() 的长度,
的长度,
∵∠COH=45°,
∴H转过的圆心角为90°,
∵OM= ![]() ,
,
则弧长= ![]() =
= ![]() =
= ![]() π.
π.
【解析】(1)证明Rt△PMC≌Rt△DMB,即可证明DB=2﹣m,AD=4﹣m,从而求解;(2)分AP=AD,PD=PA,PD=DA三种情况,根据勾股定理即可求解;(3)运动时,路线长不变,可以取当P在O点时,求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生发言次数进行了统计,并绘制成如下频数分布折线图(图1).

(1)请根据图1,回答下列问题:
①这个班共有名学生,发言次数是5次的男生有人、女生有人;
②男、女生发言次数的中位数分别是次和次;
(2)通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2所示,求第二天发言次数增加3次的学生人数和全班增加的发言总次数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF.

(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市水产养殖专业户王大爷承包了30亩水塘,分别养殖甲鱼和桂鱼,有关成本、销售情况如下表:
养殖种类
成本(万元/亩)
销售额(万元/亩)
甲鱼
2.4
3
桂鱼
2
2.5
(1)2010年,王大爷养殖甲鱼20亩,桂鱼10亩,求王大爷这一年共收益多少万元?(收益=销售额﹣成本)
(2)2011年,王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元.若每亩养殖的成本、销售额与2010年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?
(3)已知甲鱼每亩需要饲料500kg,桂鱼每亩需要饲料700kg,根据(2)中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需要全部饲料比原计划减少了2次,求王大爷原定的运输车辆每次可装载饲料多少千克? -
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=﹣2,且a≥2b,则( )
A. 有最小值
有最小值 
B. 有最大值1
有最大值1
C. 有最大值2
有最大值2
D. 有最小值
有最小值 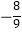
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE , 现给出下列命题正确的是( )
①若 ,则
,则  ;
;
②若DE2=BDEF,则DF=2AD.
A.①是真命题,②是真命题
B.①是真命题,②是假命题
C.①是假命题,②是真命题
D.①是假命题,②是假命题 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C,D都在⊙O上,
 的度数等于84°,CA是∠OCD的平分线,则∠ABD+∠CAO=°.
的度数等于84°,CA是∠OCD的平分线,则∠ABD+∠CAO=°. 
相关试题

