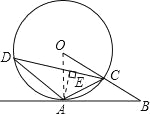
【题目】已知:如图A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,∠B=30°.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

参考答案:
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)求证:AB是⊙O的切线,可以转化为证∠OAB=90°的问题来解决.
(2)作AE⊥CD于点E,CD=DE+CE,因而就可以转化为求DE,CE的问题,根据勾股定理就可以得到.
试题解析:(1)证明:如图,连接OA;
∵OC=BC,OA=OC,
∴OA=![]() OB.
OB.
∴∠OAB=90°,
∴AB是⊙O的切线;
(2)解:作AE⊥CD于点E,
∵∠O=60°,
∴∠D=30°.
∵∠ACD=45°,AC=OC=2,
∴在Rt△ACE中,CE=AE=![]() ;
;
∵∠D=30°,
∴AD=2![]() ,
,
∴DE=![]() AE=
AE=![]() ,
,
∴CD=DE+CE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.4x+5x=9xy
B.(﹣m)3m7=m10
C.(x2y)5=x2y5
D.a12÷a8=a4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 绝对值等于3的数是﹣3
B. 绝对值不大于2的数有±2,±1,0
C. 若|a|=﹣a,则a≤0
D. 一个数的绝对值一定大于这个数的相反数
-
科目: 来源: 题型:
查看答案和解析>>【题目】一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间的平均距离,即1.4960亿km,用科学记数法表示1个天文单位是( )
A.14.960×107km
B.1.4960×108km
C.1.4960×109km
D.0.14960×109km -
科目: 来源: 题型:
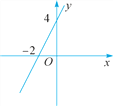
查看答案和解析>>【题目】(1)已知一次函数y=kx+b的图象经过A(0,1),B(2,0)两点,则当x_____时,y≤0.
(2)如图是一次函数y=kx+b的图象,则关于x的不等式kx+b>0的解为______.
(3)若y关于x的一次函数y=mx+n的图象不经过第四象限,则m____0,n____0.
(4)设正比例函数y=mx的图象经过点A(m,4),且函数值y随x的增大而减小,则m=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
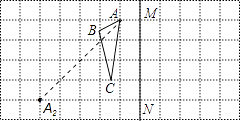
(1)请画出△ABC关于直线MN的对称图形△A1B1C1 .
(2)如果点A2是点A关于某点成中心对称,请标出这个对称中心O,并画出△ABC关于点O成中心对称的图形△A2B2C2 .
相关试题

