【题目】如图1,正方形ABCD的顶点A在原点O处,点B在x轴上,点C的坐标为(6,6),点D在y轴上,动点P,Q各从点A,D同时出发,分别沿AD,DC方向运动,且速度均为每秒1个单位长度. 
(1)探索AQ与BP有什么样的关系?并说明理由;
(2)如图2,当点P运动到线段AD的中点处时,AQ与BP交于点E,求线段CE的长.
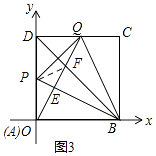
(3)如图3,设运动t秒后,点P仍在线段AD上,AQ交BD于F,且△BPQ的面积为S,试求S的最小值,及当S取最小值时∠DPF的正切值.
参考答案:
【答案】
(1)解:AQ⊥BP,AQ=BP,
理由:当点P在线段AD上时,
∵动点P,Q各从点A,D同时出发,分别沿AD,DC方向运动,且速度均为每秒1个单位长度,
∴DQ=AP,
∵四边形ABCD是正方形,
∴AD=BA,∠ADQ=∠BAP=90°,
在△ADQ和△BAP中,
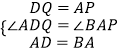 ,
,
∴△ADQ≌△BAP(SAS),
∴AQ=BP,且∠DAQ=∠ABP,
又∵∠DAQ+∠BAQ=90°,
∴∠ABP+∠BAQ=90°,
∴∠AEB=90°,
即AQ⊥BP;
当点P在AD的延长线上时,
同理可得,AQ=BP,AQ⊥BP
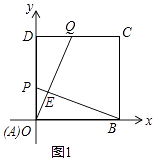
(2)解:如图2,延长AQ,BC交于点G,
当点P运动到线段AD的中点处时,AP=DQ= ![]() CD,
CD,
∴DQ=CQ,
又∵∠ADQ=∠GCQ=90°,∠AQD=∠GQC,
∴在△ADQ和△GCQ中,
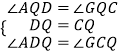 ,
,
∴△ADQ≌△GCQ(ASA),
∴AD=CG=BC,
即点C为BG的中点,
∵∠BEG=90°,
∴Rt△BEG中,EC= ![]() BG=BC=6
BG=BC=6
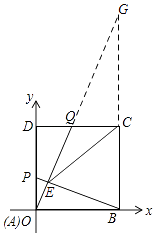
(3)解:运动t秒后,AP=DQ=t,PD=CQ=6﹣t,
∵△BPQ的面积S
=正方形ABCD的面积﹣△ABP的面积﹣△PDQ的面积﹣△BCQ的面积
=36﹣ ![]() ×6×t﹣
×6×t﹣ ![]() ×t(6﹣t)﹣
×t(6﹣t)﹣ ![]() ×6×(6﹣t)
×6×(6﹣t)
= ![]() (t﹣3)2+
(t﹣3)2+ ![]() ,
,
∴当t=3时,S取得最小值为 ![]() ,
,
且此时点P在AD的中点处,
∴DP=DQ=3,
在△DPF和△DQF中,
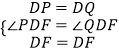 ,
,
∴△DPF≌△DQF(SAS),
∴∠DPF=∠DQF,
∵Rt△DQA中,tan∠DQA= ![]() =2,
=2,
∴tan∠DPF=2
【解析】(1)根据DQ=AP,AD=BA,∠ADQ=∠BAP=90°,即可判定△ADQ≌△BAP(SAS),进而得出AQ=BP,且∠DAQ=∠ABP,再根据∠ABP+∠BAQ=90°,可得AQ⊥BP;(2)延长AQ,BC交于点G,先判定△ADQ≌△GCQ(ASA),得出AD=CG=BC,即点C为BG的中点,再根据Rt△BEG中,EC= ![]() BG=BC,可得EC=6;(3)运动t秒后,AP=DQ=t,PD=CQ=6﹣t,根据△BPQ的面积=正方形ABCD的面积﹣△ABP的面积﹣△PDQ的面积﹣△BCQ的面积,可得S=
BG=BC,可得EC=6;(3)运动t秒后,AP=DQ=t,PD=CQ=6﹣t,根据△BPQ的面积=正方形ABCD的面积﹣△ABP的面积﹣△PDQ的面积﹣△BCQ的面积,可得S= ![]() (t﹣3)2+
(t﹣3)2+ ![]() ,进而得出当t=3时,S取得最小值为
,进而得出当t=3时,S取得最小值为 ![]() ,此时点P在AD的中点处,可判定△DPF≌△DQF(SAS),进而得到∠DPF=∠DQF,根据Rt△DQA中,tan∠DQA=
,此时点P在AD的中点处,可判定△DPF≌△DQF(SAS),进而得到∠DPF=∠DQF,根据Rt△DQA中,tan∠DQA= ![]() =2,即可得出tan∠DPF=2.
=2,即可得出tan∠DPF=2.
【考点精析】关于本题考查的二次函数的最值和正方形的性质,需要了解如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某制造企业有一座对生产设备进行水循环冷却的冷却塔,冷却塔的顶部有一个进水口,3小时恰好可以注满这座空塔,底部有一个出水口,7小时恰好可以放完满塔的水.为了保证安全,塔内剩余水量不得少于全塔水量的
 ,出水口一直打开,保证水的循环,进水口根据水位情况定时对冷却塔进行补水.假设每次恰好在剩余水量为满水量的m倍时开始补水,补满后关闭进水口.
,出水口一直打开,保证水的循环,进水口根据水位情况定时对冷却塔进行补水.假设每次恰好在剩余水量为满水量的m倍时开始补水,补满后关闭进水口.
(1)当m= 时,请问:两次补水之间相隔多长时间?每次补水需要多长时间?
时,请问:两次补水之间相隔多长时间?每次补水需要多长时间?
(2)能否找到适当的m值,使得两次补水的间隔时间和每次的补水时间一样长?如果能,请求出m值;如果不能,请你分析两次补水的间隔时间和每次的补水时间之间的数量关系,并表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】自学:如图1,△ABC中,D是BC边上一点,则△ABD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为
 =
= 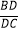 .
.
(△ABD,△ADC的面积分别用记号S△ABD , S△ADC表示)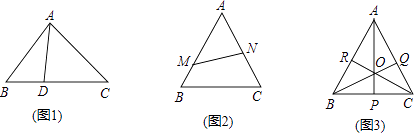
(1)心得:如图1,若BD= DC,则S△ABD:S△ADC=
DC,则S△ABD:S△ADC=
(2)成长:如图2,△ABC中,M,N分别是AB,AC边上一点,且有AM:MB=2:1,AN:NC=1:1,则△AMN与△ABC的面积比为 .
(3)巅峰:如图3,△ABC中,P,Q,R分别是BC,CA,AB边上的点,且AP,BQ,CR相交于点O,现已知△BPO,△PCO,△COQ,△AOR的面积依次为40,30,35,84,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC.
(1)如果∠AOC=50°,求∠MON的度数;
(2)如果∠AOC为任意一个锐角,你能求出∠MON的度数吗?若能,请求出来,若不能,说明为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列四个图案中,既是轴对称图形,又是中心对称图形是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校需要添置某种教学仪器,现有两种添置方法.方案1:到厂商家购买,每件需要8元和一次性的运费2000元;方案2:学校自己制作,每件4元,另外购置制作工具的费用4200元.现所需教学仪器件数不明确.
请你给校长出出主意,选择哪种方案更节约费用?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的是用4个全等的小长方形与1个小正方形密铺而成的正方形图案.已知该图案的面积为49,小正方形的面积为4,若分别用x,y(x >y)表示小长方形的长和宽,则下列关系式中不正确的是( )

A. x+y=7 B. x-y=2 C. x2 +y2=25 D. 4xy+4=49
相关试题

