【题目】解方程:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .较简便的解法是( )
.较简便的解法是( )
A. 依次用直接开平方法、配方法、公式法和因式分解法
B. ①用直接开平方法,②用公式法,③④用因式分解法
C. 依次用因式分解法、公式法、配方法和因式分解法
D. ①用直接开平方法,②③用公式法,④用因式分解法
参考答案:
【答案】D
【解析】
要看式子的特点,先看它是几项式,再看符合哪个特点从而选择合适的方法:①用直接开平方法,②③用公式法,④用因式分解法.
①3x2-12=0符合ax2=b(a,b同号且a≠0)的特点所以用直接开平方法;
②3x2-4x-2=0,等号左边有3项,方程的左边利用学过的方法不能分解,所以需要用求根公式法;
③20x2-9x-16=0,等号左边有3项,方程的左边利用学过的方法不能分解,所以需要用求根公式法;
④3(4x-1)2=7(4x-1),可以把4x-1看做是个整体,利用因式分解法解方程,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下五个方程:
①
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤
 其中一元二次方程有________(写序号)
其中一元二次方程有________(写序号) 请你选择其中的一个一元二次方程用适当的方法求出它的解.
请你选择其中的一个一元二次方程用适当的方法求出它的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Δ
 中,已知
中,已知 点
点 为
为 中点,点
中点,点 在线段
在线段 上以每秒
上以每秒 的速度由
的速度由 点向
点向 点运动,同时点
点运动,同时点 在线段
在线段 上由
上由 点向
点向 点运动。当点
点运动。当点 的运动速度为每秒____
的运动速度为每秒____ 时,能够在某一时刻使得Δ
时,能够在某一时刻使得Δ 与Δ
与Δ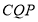 全等
全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】选取二次三项式
 中的两项,配成完全平方式的过程叫做配方.例如
中的两项,配成完全平方式的过程叫做配方.例如①选取二次项和一次项配方:
 ;
;②选取二次项和常数项配方:
 ,或
,或 ;
;③选取一次项和常数项配方:
 .
.根据上述材料,解决下面问题:
 写出
写出 的两种不同形式的配方;
的两种不同形式的配方; 若
若 ,求
,求 的值;
的值; 若关于
若关于 的代数式
的代数式 是完全平方式,求
是完全平方式,求 的值;
的值; 用配方法证明:无论
用配方法证明:无论 取什么实数时,总有
取什么实数时,总有 恒成立.
恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,
 垂直
垂直 ,AB=6,Δ
,AB=6,Δ 是等边三角形,点
是等边三角形,点 在射线
在射线 上运动,以
上运动,以 为边向右上方作等边Δ
为边向右上方作等边Δ ,射线
,射线 与射线
与射线 交于点
交于点 .
.(1)如图1,当点
 运动到与点
运动到与点 成一条直线时,
成一条直线时, (填长度),∠
(填长度),∠ 度.
度.
(2)在图2中,①求证:∠
 ;
;②随着点
 的运动,∠
的运动,∠ 的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由.
的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若
 ,
, 是关于
是关于 的方程
的方程 的两个实数根,且
的两个实数根,且 (
( 是整数),则称方程
是整数),则称方程 为“偶系二次方程”.如方程
为“偶系二次方程”.如方程 ,
, ,
, ,
, ,
, ,都是“偶系二次方程”.
,都是“偶系二次方程”. 判断方程
判断方程 是否是“偶系二次方程”,并说明理由;
是否是“偶系二次方程”,并说明理由; 对于任意一个整数
对于任意一个整数 ,是否存在实数
,是否存在实数 ,使得关于
,使得关于 的方程
的方程 是“偶系二次方程”,并说明理由.
是“偶系二次方程”,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,DC=12,AD=13,求四边形ABCD的面积.

相关试题

