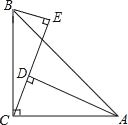
【题目】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)证明:△BCE≌△CAD;
(2)若AD=25cm,BE=8cm,求DE的长.
参考答案:
【答案】(1)证明见解析;(2)DE=17cm.
【解析】试题分析:(1)根据垂直的定义可得∠ADC=∠E=90°,然后根据同角的余角相等求出∠CBE=∠ACD,再利用“角角边”证明△BCE和△CAD全等;
(2)根据全等三角形对应边相等,通过线段的和差即可求得.
试题解析:(1)∵∠ACB=90°,BE⊥CE,AD⊥CE,
∴∠BEC=∠ACB=∠ADC=90°,
∴∠ACE+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△BCE和△CAD中, 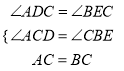 ,
,
∴△BCE≌△CAD;
(2)∵△BCE≌△CAD,
∴AD=CE,BE=CD,
∴DE=CE﹣CD=AD﹣BE=25﹣8=17(cm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
我们知道
 的几何意义是在数轴上数
的几何意义是在数轴上数 对应的点与原点的距离,即
对应的点与原点的距离,即 =
=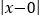 ,也就是说,
,也就是说, 表示在数轴上数
表示在数轴上数 与数0对应的点之间的距离;这个结论可以推广为
与数0对应的点之间的距离;这个结论可以推广为 表示在数轴上数
表示在数轴上数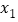 与数
与数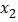 对应的点之间的距离;
对应的点之间的距离;例1.解方程|
 |=2.因为在数轴上到原点的距离为2的点对应的数为
|=2.因为在数轴上到原点的距离为2的点对应的数为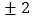 ,所以方程|
,所以方程| |=2的解为
|=2的解为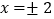 .
.例2.解不等式|
 -1|>2.在数轴上找出|
-1|>2.在数轴上找出| -1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为-1或3,所以方程|
-1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为-1或3,所以方程| -1|=2的解为
-1|=2的解为 =-1或
=-1或 =3,因此不等式|
=3,因此不等式| -1|>2的解集为
-1|>2的解集为 <-1或
<-1或 >3.
>3.
例3.解方程|
 -1|+|
-1|+| +2|=5.由绝对值的几何意义知,该方程就是求在数轴上到1和-2对应的点的距离之和等于5的点对应的
+2|=5.由绝对值的几何意义知,该方程就是求在数轴上到1和-2对应的点的距离之和等于5的点对应的 的值.因为在数轴上1和-2对应的点的距离为3(如图),满足方程的
的值.因为在数轴上1和-2对应的点的距离为3(如图),满足方程的 对应的点在1的右边或-2的左边.若
对应的点在1的右边或-2的左边.若 对应的点在1的右边,可得
对应的点在1的右边,可得 =2;若
=2;若 对应的点在-2的左边,可得
对应的点在-2的左边,可得 =-3,因此方程|
=-3,因此方程| -1|+|
-1|+| +2|=5的解是
+2|=5的解是 =2或
=2或 =-3.
=-3.
参考阅读材料,解答下列问题:
(1)方程|
 +3|=4的解为 ;
+3|=4的解为 ;(2)解不等式:|
 -3|≥5;
-3|≥5;(3)解不等式:|
 -3|+|
-3|+| +4|≥9
+4|≥9 -
科目: 来源: 题型:
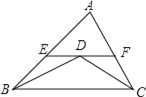
查看答案和解析>>【题目】如图,△ABC中,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,与AB、AC分别相交于E、F,若已知AB=9,AC=7,求△AEF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点A处,测得河的南岸边点B在其南偏东45°方向,然后向北走20米到达C点,测得点B在点C的南偏东33°方向,求出这段河的宽度(结果精确到1米,参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,
 ≈1.41)
≈1.41)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x+b与反比例函数y=
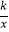 的图形交于A(a,4)和B(4,1)两点.
的图形交于A(a,4)和B(4,1)两点. 
(1)求b,k的值;
(2)在第一象限内,当一次函数y=﹣x+b的值大于反比例函数y=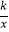 的值时,直接写出自变量x的取值范围;
的值时,直接写出自变量x的取值范围;
(3)将直线y=﹣x+b向下平移m个单位,当直线与双曲线只有一个交点时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点D为△ABC边BC的延长线上一点.

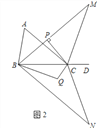
(1)若∠A∶∠ABC=3∶4,∠ACD=140°,求∠A的度数;
(2)若∠ABC的角平分线与∠ACD的角平分线交于点M,过点C作CP⊥BM于点P.
求证:
 ;
;(3)在(2)的条件下,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q(如图2),试探究∠BQC与∠A有怎样的数量关系,请写出你的猜想并证明.
-
科目: 来源: 题型:
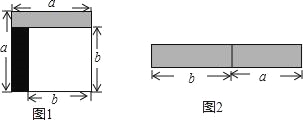
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2
B、a2﹣b2=(a+b)(a﹣b)
C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x﹣2y的值.
②计算:(1﹣
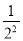 )(1﹣
)(1﹣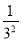 )(1﹣
)(1﹣ )…(1﹣
)…(1﹣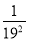 )(1﹣
)(1﹣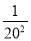 ).
).
相关试题

