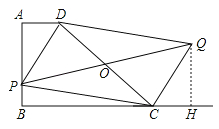
【题目】如图四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,P为AB边上的一动点,以PD,PC为边作平行四边形PCQD,则对角线PQ的长的最小值是( )

A.3B.4C.5D.6
参考答案:
【答案】B
【解析】
过点Q作QH⊥BC,交BC的延长线于H,如图,根据AAS易证得Rt△ADP≌Rt△HCQ,可得AD=HC,进而可求得BH的长,则可得当PQ⊥AB时,PQ的长最小,即为BH的长.
解:过点Q作QH⊥BC,交BC的延长线于H,如图,
∵AD∥BC,
∴∠ADC=∠DCH,即∠ADP+∠PDC=∠DCQ+∠QCH,
∵PD∥CQ,
∴∠PDC=∠DCQ,
∴∠ADP=∠QCH,
又∵PD=CQ,∠A=∠CHQ=90°,
∴Rt△ADP≌Rt△HCQ(AAS),
∴AD=HC,
∵AD=1,BC=3,
∴BH=4,
∴当PQ⊥AB时,PQ的长最小,即为4.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x+1与x轴,y轴分别交于B,A两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°交x轴于点Q.

(1)求点A和点B的坐标;
(2)比较∠AOP与∠BPQ的大小,说明理由.
(3)是否存在点P,使得△OPQ是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号中:8,﹣
 ,+2.8,π,
,+2.8,π, ,﹣0.003,0,﹣100,﹣3.626626662……
,﹣0.003,0,﹣100,﹣3.626626662……正数集合{_____ …}
整数集合{_____…}
负分数集合{_____ …}
无理数集合{_____ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活与数学
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
(1)姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是48,那么这四个数是_______.
(2)丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是46,则它们分别是_____.
(3)莉也在日历上圈出5个数,呈十字框形,它们的和是55,则中间的数是______.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是______号?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n=
 .
.
如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级有500名学生,从中随机抽取了一部分学生,统计每晚写作业的时间,根据它们的时间(单位:分钟),绘制出如下的统计图①和图②请根据相关信息,解答下列问题:

(1)图①中m=________,n=________;
(2)求统计的这组数据的平均数、众数和中位数;
(3)根据样本数据,估计这500名学生中,时间为120分钟的约有多少学生?
-
科目: 来源: 题型:
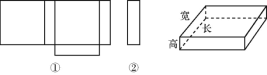
查看答案和解析>>【题目】小明在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了几条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:已知这个长方体纸盒高为20 cm,底面是一个正方形,并且这个长方体纸盒所有棱长的和是880 cm,求这个长方体纸盒的体积.
相关试题

