【题目】如图,在正方形ABCD中,E,F分别BC,CD边上的一点,且BE=2EC,FC=![]() DC,连接AE,AF,EF,求证:△AEF是直角三角形.
DC,连接AE,AF,EF,求证:△AEF是直角三角形.

参考答案:
【答案】见解析.
【解析】
设FC=2a,由正方形的性质得出AB=BC=AD=CD=9a,![]() ,然后利用勾股定理分别表示出
,然后利用勾股定理分别表示出![]() ,然后根据勾股定理的逆定理即可证明结论.
,然后根据勾股定理的逆定理即可证明结论.
证明:设FC=2a,则DC=9a,DF=7a.
∵四边形ABCD是正方形,
∴AB=BC=AD=CD=9a,![]() .
.
∵BE=2CE,
∴BE=6a,EC=3a.
在Rt△ECF中,EF2=EC2+FC2=(3a)2+(2a)2=13a2.
在Rt△ADF中,AF2=AD2+DF2=(9a)2+(7a)2=130a2.
在Rt△ABE中,AE2=AB2+BE2=(9a)2+(6a)2=117a2.
∵13a2+117a2=130a2,
∴EF2+AE2=AF2.
∴△AEF是以∠AEF为直角的直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用两种正多边形铺满地面,其中一种是正八边形,则另一种正多边形是( )。
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=450;③CE=2DE;④AG∥CF;⑤S△FGC=
 .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(﹣4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=
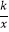 (k>0,x>0)的图象经过点C,则k的值为( )
(k>0,x>0)的图象经过点C,则k的值为( )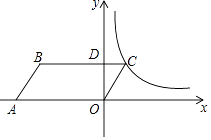
A.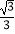
B.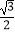
C.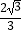
D.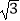
-
科目: 来源: 题型:
查看答案和解析>>【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西30°方向航行10km至C港.
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据:
 ≈1.414,
≈1.414, ≈1.732);
≈1.732);(2)确定C港在A港的什么方向.

相关试题

