【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的
有两个实数根,且其中一个根为另一个根的![]() 倍,那么称这样的方程为“倍根方程”,例如,一元二次方程
倍,那么称这样的方程为“倍根方程”,例如,一元二次方程![]() 的两个根是
的两个根是![]() 和
和![]() ,则方程
,则方程![]() 就是“倍根方程”.
就是“倍根方程”.
(1)若一元二次方程![]() 是“倍根方程”,则
是“倍根方程”,则![]() = .
= .
(2)若关于![]() 的一元二次方程
的一元二次方程![]() 是“倍根方程”,则
是“倍根方程”,则![]() ,
,![]() ,
,![]() 之间的关系为 .
之间的关系为 .
(3)若![]() 是“倍根方程”,求代数式
是“倍根方程”,求代数式![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)0
;(3)0
【解析】
(1)根据“倍根方程”和根与系数之间的关系可直接求解.
(2)根据题目信息和根与系数的关系找出m,n之间的关系,再对代数式求解.
(3)根据倍根方程的定义找出m,n之间的关系,进行分类讨论即可求解.
(1)∵一元二次方程![]() 是“倍根方程”
是“倍根方程”
∴令2x1=x2,有x1+ x2=3,x1x2=c
∴c=2
(2)设x=m,x=2m是方程![]() 的解
的解
∴2m+m=-![]() ,2m2=
,2m2=![]()
消去m解得2b2=9ac
所以![]() ,
,![]() ,
,![]() 之间的关系为
之间的关系为![]()
(3)∵![]() 是“倍根方程”
是“倍根方程”
∴方程的两个根分别为x=2和x=![]() ,
,
∴![]() =4或
=4或![]() =1,即n=4m或n=m
=1,即n=4m或n=m
当n=4m时,原式为(m-n)(4m-n)=0,
当n=m时,原式为(m-n)(4m-n)=0,
∴代数式![]() =0
=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,DE平分∠ADC交BC边于点E,P为DE上的一点(PE<PD),PM⊥PD,PM交AD边于点M.
(1)若点F是边CD上一点,满足PF⊥PN,且点N位于AD边上,如图1所示.
求证:①PN=PF;②DF+DN=
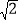 DP;
DP;(2)如图2所示,当点F在CD边的延长线上时,仍然满足PF⊥PN,此时点N位于DA边的延长线上,如图2所示;试问DF,DN,DP有怎样的数量关系,并加以证明.
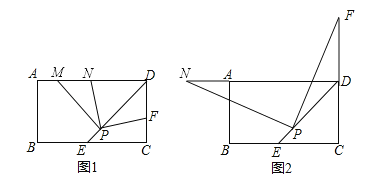
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC和CD于点P,Q.
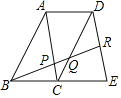
(1)求证:△ABP∽△DQR;
(2)求
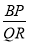 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
-
科目: 来源: 题型:
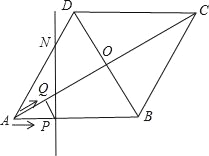
查看答案和解析>>【题目】如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2
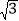 cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.(1)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC 中,∠C=90°,∠B=30°,以点 A 为圆心,任意长为半径画弧分别交 AB,AC 于点M 和 N,再分别以 M,N 为圆心,大于
 MN的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2,正确的序号是_____.
MN的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2,正确的序号是_____.
相关试题

