【题目】如图,已知![]() 两点的坐标分别为
两点的坐标分别为![]() 将线段
将线段![]() 向右平移
向右平移![]() 个单位到线段
个单位到线段![]() 连接
连接![]() 得四边形
得四边形![]() .
.
(1)则点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ,
的坐标为 ,![]() ;
;
(2)如图①,若点![]() 为四边形
为四边形![]() 内的一点,且
内的一点,且![]() 求
求![]() 的值.
的值.

(3)如图②,若点![]() 为四边形
为四边形![]() 内的一点(包括边界).且
内的一点(包括边界).且![]() 当
当![]() 面积取最大值时,求此时对应的点
面积取最大值时,求此时对应的点![]() 的坐标和最大面积的值.[提示:
的坐标和最大面积的值.[提示:![]() ]
]
参考答案:
【答案】(1)![]() ,
,![]() ,12;(2)
,12;(2)![]() ;(3)当
;(3)当![]() 时,△PAC的面积最大,最大面积值为
时,△PAC的面积最大,最大面积值为![]() .
.
【解析】
(1)利用平移的性质,平行四边形的面积公式解决问题即可.
(2)如图①中,过点![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .根据
.根据![]() ,构建方程解决问题即可.
,构建方程解决问题即可.
(3)作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .利用面积法求出
.利用面积法求出![]() ,
,![]() 的坐标,求出△
的坐标,求出△![]() ,△
,△![]() 的面积比较即可判断.
的面积比较即可判断.
(1)![]() ,
,![]() ,线段
,线段![]() 向右平移4个单位得到线段
向右平移4个单位得到线段![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,根据平移的规律得:
是平行四边形,根据平移的规律得:![]() ,
,![]() ,
,
![]() ,
,
(2)如图①,过![]() 作
作![]() 轴
轴
则![]()
![]()
即![]()
解得![]()
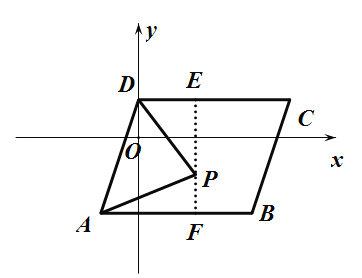
(3)作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
同法可得![]() ,
,
![]() ,
,
![]() 当
当![]() ,
,![]() 时,
时,![]() 的面积最大,最大值为4.
的面积最大,最大值为4.
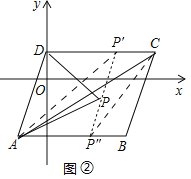
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用4400元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
类型价格
A型
B型
进价(元/件)
60
100
标价(元/件)
100
160
(1)请利用二元一次方程组求这两种服装各购进的件数;
(2)如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则
 的值为 .
的值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
-
科目: 来源: 题型:
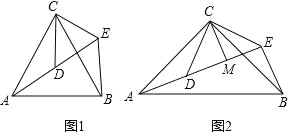
查看答案和解析>>【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:
①∠AEB的度数为______;
②线段AD,BE之间的数量关系为______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】寿县教育部门计划在3月12日植树节当天安排
 ,
, 两校部分学生到森林公园参加植树活动.已知
两校部分学生到森林公园参加植树活动.已知 校区的每位学生往返车费是6元,
校区的每位学生往返车费是6元, 校每位学生的往返车费是10元,要求两所学校均要有学生参加,且
校每位学生的往返车费是10元,要求两所学校均要有学生参加,且 校参加活动的学生比
校参加活动的学生比 校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求
校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求 ,
, 两校最多各有多少学生参加?
两校最多各有多少学生参加?
相关试题

