【题目】如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AECD=ADCE. 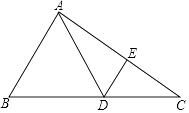
(1)求证:DE∥AB;
(2)如果点F是DE延长线上一点,且BD是DF和AB的比例中项,联结AF.求证:DF=AF.
参考答案:
【答案】
(1)证明:∵AECD=ADCE,
∴ ![]() ,
,
∵∠DAB=∠B,
∴AD=BD,
∴ ![]() ,
,
∴DE∥AB;
(2)证明:∵BD是DF和AB的比例中项,
∴BD2=DFAB,
∵AD=BD,
∴AD2=DFAB,
∴ ![]() ,
,
∵DE∥AB,
∴∠ADF=∠BAD,
∴△ADF∽△DBA,
∴ ![]() =1,
=1,
∴DF=AF.
【解析】(1)根据已知条件得到 ![]() ,根据等腰三角形的判定定理得到AD=BD,等量代换即可得到结论;(2)由BD是DF和AB的比例中项,得到BD2=DFAB,等量代换得到AD2=DFAB,推出
,根据等腰三角形的判定定理得到AD=BD,等量代换即可得到结论;(2)由BD是DF和AB的比例中项,得到BD2=DFAB,等量代换得到AD2=DFAB,推出 ![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到 ![]() =1,于是得到结论.
=1,于是得到结论.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,AB=AC=5,BC=8,∠PDQ的顶点D在BC边上,DP交AB边于点E,DQ交AB边于点O且交CA的延长线于点F(点F与点A不重合),设∠PDQ=∠B,BD=3.
(1)求证:△BDE∽△CFD;
(2)设BE=x,OA=y,求y关于x的函数关系式,并写出定义域;
(3)当△AOF是等腰三角形时,求BE的长.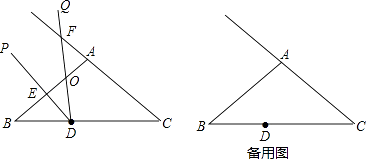
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D、E分别在边AB、AC上,联结DE,那么下列条件中不能判断△ADE和△ABC相似的是( )
A.DE∥BC
B.∠AED=∠B
C.AE:AD=AB:AC
D.AE:DE=AC:BC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=3,BC=2,点D是边AB上的动点,过点D作DE∥BC,交边AC于点E,点Q是线段DE上的点,且QE=2DQ,连接BQ并延长,交边AC于点P.设BD=x,AP=y.
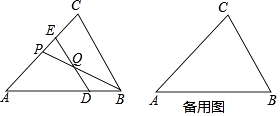
(1)求y关于x的函数解析式及定义域;
(2)当△PQE是等腰三角形时,求BD的长;
(3)连接CQ,当∠CQB和∠CBD互补时,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处.

(1)求该海轮从A处到B处的航行过程中与小岛C之间的最短距离(记过保留根号);
(2)如果该海轮以每小时20海里的速度从B处沿BC方向行驶,求它从B处到达小岛C的航行时间(结果精确到0.1小时).(参考数据: =1.41,
=1.41,  =1.73)
=1.73) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设
 =
=  ,
, 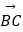 =
= 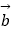 .求:
.求: 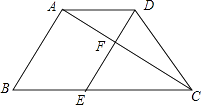
(1)向量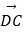 (用向量
(用向量  、
、 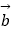 表示);
表示);
(2)tanB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣4x+4沿y轴向下平移9个单位,所得新抛物线与x轴正半轴交于点B,与y轴交于点C,顶点为D.求:(1)点B、C、D坐标;(2)△BCD的面积.
相关试题

