【题目】在△ABC中,点D、E分别在边AB、AC上,联结DE,那么下列条件中不能判断△ADE和△ABC相似的是( )
A.DE∥BC
B.∠AED=∠B
C.AE:AD=AB:AC
D.AE:DE=AC:BC
参考答案:
【答案】D
【解析】解:如图, 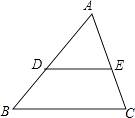
A、∵DE∥BC,
∴△ADE∽△ABC,故本选项错误;
B、∵∠AED=∠B,∠A=∠A,
∴△ADE∽△ACB,故本选项错误;
C、∵AE:AD=AB:AC,∠A=∠A,
∴△ADE∽△ACB,故本选项错误;
D、AE:DE=AC:BC不能使△ADE和△ABC相似,故本选项正确.
故选D.
【考点精析】解答此题的关键在于理解相似三角形的判定的相关知识,掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,点E在CB的延长线上,联结AE、DE,DE与边AB交于点F,FG∥BE且与AE交于点G.
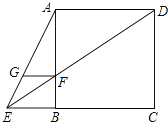
(1)求证:GF=BF.
(2)在BC边上取点M,使得BM=BE,联结AM交DE于点O.求证:FOED=ODEF. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=﹣x2+2bx+c与x轴交于点A、B(点A在点B的右侧),且与y轴正半轴交于点C,已知A(2,0)
(1)当B(﹣4,0)时,求抛物线的解析式;
(2)O为坐标原点,抛物线的顶点为P,当tan∠OAP=3时,求此抛物线的解析式;
(3)O为坐标原点,以A为圆心OA长为半径画⊙A,以C为圆心, OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式.
OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,AB=AC=5,BC=8,∠PDQ的顶点D在BC边上,DP交AB边于点E,DQ交AB边于点O且交CA的延长线于点F(点F与点A不重合),设∠PDQ=∠B,BD=3.
(1)求证:△BDE∽△CFD;
(2)设BE=x,OA=y,求y关于x的函数关系式,并写出定义域;
(3)当△AOF是等腰三角形时,求BE的长.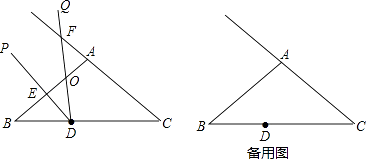
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=3,BC=2,点D是边AB上的动点,过点D作DE∥BC,交边AC于点E,点Q是线段DE上的点,且QE=2DQ,连接BQ并延长,交边AC于点P.设BD=x,AP=y.
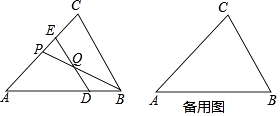
(1)求y关于x的函数解析式及定义域;
(2)当△PQE是等腰三角形时,求BD的长;
(3)连接CQ,当∠CQB和∠CBD互补时,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AECD=ADCE.
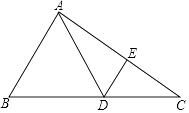
(1)求证:DE∥AB;
(2)如果点F是DE延长线上一点,且BD是DF和AB的比例中项,联结AF.求证:DF=AF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处.

(1)求该海轮从A处到B处的航行过程中与小岛C之间的最短距离(记过保留根号);
(2)如果该海轮以每小时20海里的速度从B处沿BC方向行驶,求它从B处到达小岛C的航行时间(结果精确到0.1小时).(参考数据: =1.41,
=1.41,  =1.73)
=1.73)
相关试题

