【题目】如图△ABC中,∠BAC=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为_______.

参考答案:
【答案】69°
【解析】
在BC下方取一点D,使得三角形ABD为等边三角形,连接DP、DC,根据等边三角形的性质得到AD=AB=AC,求出∠DAC、∠ACD、∠ADC的度数,根据三角形的内角和定理求出∠ABC=∠ACB=51°,即∠CDB=141°=∠BPC,再证△BDC≌△BPC,得到PC=DC,进一步得到等边△DPC,推出△APD≌△APC,根据全等三角形的性质得到∠DAP=∠CAP=9°,即可求出答案.
在BC下方取一点D,使得三角形ABD为等边三角形,连接DP、DC
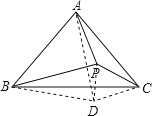
∴AD=AB=AC,![]()
![]()
∴![]()
∵![]()
∴![]()
∴![]()
又∵![]()
∴△BDC≌△BPC,
∴PC=DC,
又∵![]()
∴△DPC是等边三角形,
∴△APD≌△APC,
∴![]()
∴![]()
故答案为:69°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】取一副三角板按如图所示拼接,固定三角板ADC,将三角板ABC绕点A顺时针方向旋转,旋转角度为α(0°<α≤45°),得到△ABC′.

①当α为多少度时,AB∥DC?
②当旋转到图③所示位置时,α为多少度?
③连接BD,当0°<α≤45°时,探求∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,则BD的长为( )

A. 5cm B. 6cm C. 7cm D. 8cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )

A. 25° B. 30° C. 35° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A 的度数.

相关试题

