搜索
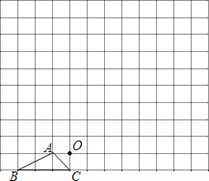
【题目】小方格都是边长为1的正方形，△ABC的顶点和O点都在正方形的顶点上．
（1）以点O为位似中心，在方格图中将△ABC放大为原来的2倍，得到△A′B′C′；
（2）△A′B′C′绕点B′顺时针旋转90°，画出旋转后得到的△A″B′C″，并求边A′B′在旋转过程中扫过的图形面积．
参考答案：
【答案】（1）见解析；（2）5π（平方单位）．
【解析】（1）连接AO、BO、CO并延长到2AO、2BO、2CO长度找到各点的对应点，顺次连接即可．
（2）△A′B′C′的A′、C′绕点B′顺时针旋转90°得到对应点，顺次连接即可．A′B′在旋转过程中扫过的图形面积是一个扇形，根据扇形的面积公式计算即可．
解：（1）见图中△A′B′C′
（直接画出图形，不画辅助线不扣分）
（2）见图中△A″B′C″
（直接画出图形，不画辅助线不扣分）
S=
π（22+42）=
π20=5π（平方单位）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若10m=5，10n=3，则102m+3n= ．
【答案】675．
【解析】102m+3n=102m103n=(10m)2(10n)3=5233=675，
故答案为：675.
点睛：此题考查了幂的乘方与积的乘方, 同底数幂的乘法. 首先根据同底数幂的乘法法则，可得102m+3n=102m×103n，然后根据幂的乘方的运算方法，可得102m×103n=（10m）2×（10n）3，最后把10m=5，10n=2代入化简后的算式，求出102m+3n的值是多少即可．
【题型】填空题
【结束】
18【题目】计算：
（1）（5mn2﹣4m2n）（﹣2mn）
（2）（x+7）（x﹣6）﹣（x﹣2）（x+1）
（3） (－
)2 016×161 008； -
科目： 来源： 题型：
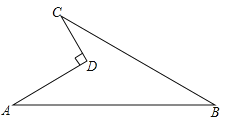
查看答案和解析>>【题目】如图所示的一块地，已知AD=4m，CD=3m，∠ADC=90°，AB=13m，BC=12m，求这块地的面积．
-
科目： 来源： 题型：
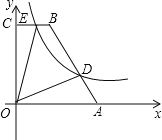
查看答案和解析>>【题目】如图，在直角梯形OABC中，BC∥AO，∠AOC=90°，点A，B的坐标分别为（5，0）， （2，6），点D为AB上一点，且BD=2AD，双曲线y=
（k＞0）经过点D，交BC于点E．（1）求双曲线的解析式；
（2）求四边形ODBE的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若(a﹣b)2=4，ab=5，则(a+b)2=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）（5mn2﹣4m2n）（﹣2mn）
（2）（x+7）（x﹣6）﹣（x﹣2）（x+1）
（3） (－
)2 016×161 008；【答案】（1）﹣10m2n3+8m3n2；（2）2x﹣40；(3)1．
【解析】试题分析：（1）原式利用单项式乘以多项式法则计算即可得到结果；
（2）原式两项利用多项式乘以多项式法则计算，去括号合并即可得到结果；
（3）先根据幂的乘方的逆运算，把(－
)2 016化为(
)1008，再根据积的乘方的逆运算计算即可.试题解析：（1）原式=（5mn2）（﹣2mn）+（﹣4m2n）（﹣2mn）=﹣10m2n3+8m3n2；
（2）原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40．
（3）原式=(
)1008×161 008=(
×16)1 008=1.【题型】解答题
【结束】
19【题目】如图，方格图中每个小正方形的边长为1，点A、B、C都是格点．
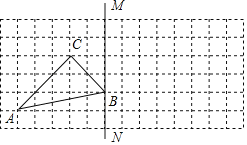
（1）画出△ABC关于直线BM对称的△A1B1C1；
（2）写出AA1的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一幅长60 cm、宽40 cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是2 816 cm2，设金色纸边的宽为x cm，那么x满足的方程是( )
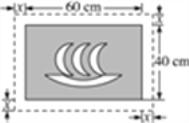
A. (60＋x)(40＋2x)＝2 816 B. (60＋x)(40＋x)＝2 816
C. (60＋2x)(40＋x)＝2 816 D. (60＋2x)(40＋2x)＝2 816
相关试题
