【题目】如图是某月的月历

(1)如图1,带阴影的方框中的9个数的和与方框中心的数有什么关系?并试着说明理由;
(2)如果将阴影的方框移至图2的位置,(1)中关系的关系还成立吗?并试着说明理由;
(3)不改变阴影方框的大小,将方框移动几个位置试一试,你能得出什么结论?并说明理由.
参考答案:
【答案】(1)带阴影的方框中的9个数的和是方框中心的数的9倍;(2)(1)关系的关系成立.理由见解析;(3)移动位置,方框中9个数之和为方框正中心数的9倍.理由见解析.
【解析】
(1)求出9个数之和,然后找出与正中心的数的关系:带阴影的方框中的9个数的和是方框中心的数的9倍;
(2)改变位置,关系不变.仿照(1)计算即可;
(3)设方框中心的数为x,根据表格依次写出其他9个数字,然后相加得出关系.
解:(1)带阴影的方框中的9个数的和是方框中心的数的9倍
因为3+4+5+10+11+12+17+18+19=99=11×9
所以带阴影的方框中的9个数的和是方框中心的数的9倍.
(2)答:(1)关系的关系成立.
因为8+9+10+15+16+17+22+23+24=144=16×9
所以带阴影的方框中的9个数的和是方框中心的数的9倍,
改变位置,关系不变.
(3)不改变阴影方框的大小,将方框移动几个位置,关系不变,
带阴影的方框中的 9个数之和是方框中心数的9倍.
设方框中心的数为x,
则(x﹣8)+(x﹣7)+(x﹣6)+(x﹣1)+x+(x+1)+(x+6)+(x+7)+(x+8)=9x.
所以带阴影的方框中的9个数的和是方框中心的数的9倍.
故移动位置,方框中9个数之和为方框正中心数的9倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
-
科目: 来源: 题型:
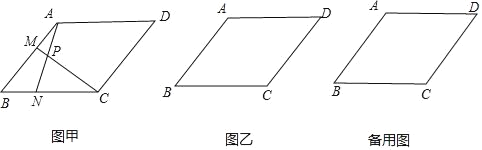
查看答案和解析>>【题目】在ABCD中,AB=BC=9,∠BCD=120°.点M从点A出发沿射线AB方向移动.同时点N从点B出发,以相同的速度沿射线BC方向移动,连接AN,CM,直线AN、CM相交于点P.
(1)如图甲,当点M、N分别在边AB、BC上时,
①求证:AN=CM;
②连接MN,当△BMN是直角三角形时,求AM的值.
(2)当M、N分别在边AB、BC的延长线上时,在图乙中画出点P,并直接写出∠CPN的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=k1x+b与反比例函数y=
 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b>
 的解集;
的解集;(3)若P(p,y1),Q(﹣2,y2)是函数y=
 图象上的两点, 且y1>y2,求实数p的取值范围.
图象上的两点, 且y1>y2,求实数p的取值范围.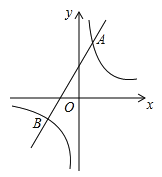
-
科目: 来源: 题型:
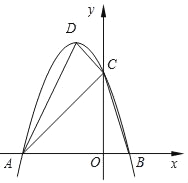
查看答案和解析>>【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与x轴交于点A和点B(1,0),与y轴相交于点C(0,3).
(1)求抛物线的解析式和顶点D的坐标;
(2)求证:∠DAB=∠ACB;
(3)点Q在抛物线上,且△ADQ是以AD为底的等腰三角形,求Q点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC中,AB=AC,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O,点M,N分别为线段BO和CO的中点.求证:四边形EDNM是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.

相关试题

