【题目】如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论不一定成立的是( )
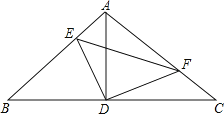
A.△ADF≌△BDE
B.S四边形AEDF=![]() S△ABC
S△ABC
C.BE+CF=![]() AD
AD
D.EF=AD
参考答案:
【答案】D
【解析】
试题分析:根据等腰直角三角形的性质得到AD=BD=CD,∠ADB=∠ADC=90°,∠B=∠C=∠BAD=∠CAD=45°,根据余角的性质得到∠BDE=∠ADF,于是得到△ADF≌△BDE,证得S△ADF=S△BDE,推出S四边形AEDF=S△ADE+S△ADF=S△ADE+S△BDE﹣S△ABD,得到S四边形AEDF=![]() S△ABC,根据全等三角形的性质得到AF=BE,等量代换得到BE+CF=AF+CF=AC=
S△ABC,根据全等三角形的性质得到AF=BE,等量代换得到BE+CF=AF+CF=AC=![]() AD,由等腰直角三角形的性质得到AD=
AD,由等腰直角三角形的性质得到AD=![]() BC,当EF∥BC时,EF=
BC,当EF∥BC时,EF=![]() BC,而EF不一定平行于BC,即可得到结论.
BC,而EF不一定平行于BC,即可得到结论.
解:∵∠BAC=90°,AB=AC,点D为BC的中点,
∴AD=BD=CD,∠ADB=∠ADC=90°,∠B=∠C=∠BAD=∠CAD=45°,
∵∠EDF=90°,
∴∠BDE+∠ADE=∠ADE+∠ADF=90°,
∴∠BDE=∠ADF,
在△ADF与△BDE中,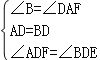 ,
,
∴△ADF≌△BDE,
∴S△ADF=S△BDE,
∵S四边形AEDF=S△ADE+S△ADF=S△ADE+S△BDE﹣S△ABD,
∵S△ABD=![]() S△ABC,
S△ABC,
∴S四边形AEDF=![]() S△ABC,
S△ABC,
∵△ADF≌△BDE,
∴AF=BE,
∴BE+CF=AF+CF=AC=![]() AD,
AD,
∵AD=![]() BC,
BC,
当EF∥BC时,EF=![]() BC,
BC,
而EF不一定平行于BC,
∴EF不一定等于![]() BC,
BC,
∴EF≠AD,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距108千米,甲、乙两人分别从A、B两地同时出发,相向而行,甲的速度为14千米/小时,乙的速度为22千米/小时,经过_________小时后两人相距36千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知二次函数y=ax2图象的顶点为原点,直线y=
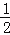 x+4的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.
x+4的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.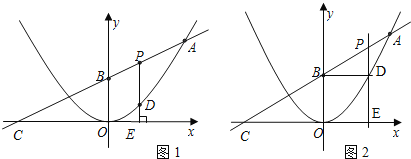
(1)求这个二次函数的解析式与B点坐标;
(2)P为线段AB上的一个动点(点P与A,B不重合),过P作x轴的垂线与这个二次函数的图象交于D点,与x轴交于点E.设线段PD的长为h,点P的横坐标为t,求h与t之间的函数关系式,并写出自变量t的取值范围(图1);
(3)在(2)的条件下,连接BD,当动点P在线段AB上移动时,点D也在抛物线上移动,线段BD也绕点B转动,当BD∥x轴时(图2),请求出P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D…的规律绕在ABCD的边上,则细线另一端所在位置的点的坐标是( )

A. (0,-2) B. (-1,-1) C. (-1,0) D. (1,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,点A,B,C均在格点上.
(1)请值接写出点A,B,C的坐标.
(2)若平移线段AB,使B移动到C的位置,请在图中画出A移动后的位置D,依次连接B,C,D,A,并求出四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a表示一个任意有理数,那么下面说法正确的是( )
A. ﹣a是负数 B. |a|一定是正数 C. |a|一定不是负数 D. |﹣a|一定是负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆锥底面圆的半径为3m,其侧面展开图是半圆,则圆锥母线长为m.
相关试题

