【题目】y= ![]() x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0的根的情况为( )
x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0的根的情况为( )
A.没有实数根
B.有一个实数根
C.有两个不相等的实数根
D.有两个相等的实数根
参考答案:
【答案】A
【解析】解:
∵y= ![]() x+1是关于x的一次函数,
x+1是关于x的一次函数,
∴ ![]() ≠0,
≠0,
∴k﹣1>0,解得k>1,
又一元二次方程kx2+2x+1=0的判别式△=4﹣4k,
∴△<0,
∴一元二次方程kx2+2x+1=0无实数根,
所以答案是:A.
【考点精析】通过灵活运用求根公式和一次函数的概念,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一般地,如果y=kx+b(k,b是常数,k不等于0),那么y叫做x的一次函数即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】早晨
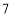 点,小明乘车从学校出发,去卧龙大熊猫自然保护区参观,当天按原路返回.如图,是小明出行的过程中,他距卧龙大熊猫自然保护区的距离
点,小明乘车从学校出发,去卧龙大熊猫自然保护区参观,当天按原路返回.如图,是小明出行的过程中,他距卧龙大熊猫自然保护区的距离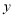 (千米)与他离校的时间
(千米)与他离校的时间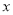 (小时)之间的图象.根据图象,完成下面问题:
(小时)之间的图象.根据图象,完成下面问题:(1)小明乘车去保护区的速度是_________千米/小时,
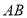 线段所表示的
线段所表示的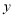 与
与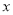 的关系式是_________;
的关系式是_________;(2)已知下午
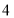 点,小明距保护区
点,小明距保护区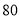 千米,问他何时才能回到学校?
千米,问他何时才能回到学校?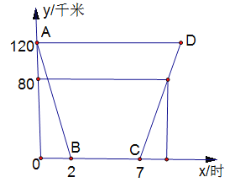
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形
 中,
中, ,
, ,
, ,
, 是
是 边上的中线,过点
边上的中线,过点 作
作 垂足为
垂足为 ,
, 交线段
交线段 于点
于点 ,交
,交 于点
于点 ,连接
,连接 .
.(1)求证:
 ;
;(2)探索线段
 和
和 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;(3)当
 等于多少度时,点
等于多少度时,点 恰好为
恰好为 中点?
中点?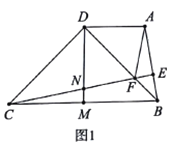
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
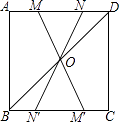
A.2对
B.3对
C.4对
D.5对 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
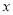 的不等式组
的不等式组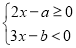 整数解为1、2,如果把适合这个不等式组的整数
整数解为1、2,如果把适合这个不等式组的整数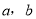 组成有序数对
组成有序数对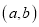 ,那么对应在平面直角坐标系上的点共有的个数为_______.
,那么对应在平面直角坐标系上的点共有的个数为_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(
 ,0),有下列结论:①abc>0;
,0),有下列结论:①abc>0;
②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0; ⑤a﹣b≥m(am﹣b);
其中所有正确的结论是( )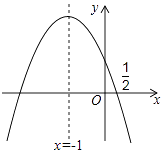
A.①②③
B.①③④
C.①②③⑤
D.①③⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,EG∥AD,找出图中的等腰三角形,并给出证明.
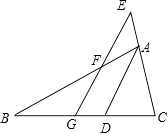
相关试题

