【题目】如图,A(0,1),M(3,2),N(4,4) , 动点P从点A出发,沿y
轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为 t 秒.(直线y = kx+b平移时k不变)

(1)当t=3时,求 l 的解析式;
(2)若点M,N位于l 的异侧,确定 t 的取值范围.
参考答案:
【答案】(1)y=-x+4;(2)4<t<7.
【解析】
试题分析:(1)将A点的坐标代入可得b=1,根据平移可得b=1+t,将t=3代入求出b的值;(2)、将点M和N分别代入解析式分别求出t的值,得出范围.
试题解析:(1)直线y=-x+b交y轴于点P(0,b),由题意,得b>0,t≥0,b=1+t
当t=3时,b=4 ∴y=-x+4
(2)当直线y=-x+b过M(3,2)时,2=-3+b解得b=5,
∴5=1+t
∴t=4
当直线y=-x+b过N(4,4)时,4=-4+b解得 b=8
∴8=1+t
∴t=7
∴4<t<7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x+3与x轴,y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,点A在点B的左边,顶点为P,且线段AB的长为2.
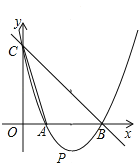
(1)求点A的坐标;
(2)求该抛物线的函数表达式;
(3)在抛物线的对称轴上是否存在点G,使|GC﹣GB|最大?若存在,求G点坐标;若不存在说明理由.
(4)连结AC,请问在x轴上是否存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数
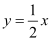 的图象相交于点(2,a).
的图象相交于点(2,a).
(1)求a的值.
(2)求一次函数y=kx+b的表达式.
(3)在同一坐标系中,画出这两个函数的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
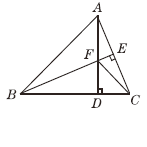
(1)求证:BF=2AE;
(2)若CD=
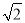 ,求AD的长.
,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:求1+2+22+23+24+…22013的值.
解:设S=1+2+22+23+24+…+22012+22013,将等式两边同时乘以2得:
2S=2+22+23+24+25+…+22013+22014,将下式减去上式得:
2S﹣S=22014﹣1,即S=22014﹣1,即1+2+22+23+24+…22013=﹣1
请你仿照此法计算1+3+32+33+34…+32014的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】钓鱼岛是我国渤海海峡上的一颗明珠,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向钓鱼岛驶来,渔船向渔政部门报告,并立即返航.渔政船接到报告后,立即从该港口出发赶往钓鱼岛.下图是渔船及渔政船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)

(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.]
(2)求渔船和渔政船相遇时,两船与钓鱼岛的距离.
(3)在渔政船驶往钓鱼岛的过程中,求渔船从港口出发经过多长时间与渔政船相距30海里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式乘法算式中,可以用平方差公式计算的是( )
A. (m﹣n)(n﹣m) B. (a+b)(﹣a﹣b) C. (﹣a﹣b)(a﹣b) D. (a+b)(a+b)
相关试题

