Question

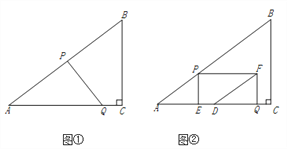
【题目】如图①，在Rt△ABC中，∠C=90°，AB=10，BC=6．点P从点A出发，沿折现AB—BC向终点C运动，在AB上以每秒5个单位长度的速度运动，在BC上以每秒3个单位长度的速度运动．点Q从点C出发，沿CA方向以每秒个单位长度的速度运动．点P、Q两点同时出发，当点P停止时，点Q也随之停止．设点P运动的时间为t秒．

（1）求线段AQ的长．（用含t的代数式表示）

（2）当PQ与△ABC的一边平行时，求t的值

（3）如图②，过点P作PE⊥AC于点E，以PE、QE为邻边作矩形PEQF，点D为AC的中点，连结DF．直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值．

Answer 1

【答案】（1）AQ=8-t（0≤t≤4）；

（2）t=s或3s时，当PQ与△ABC的一边平行；

（3）①S=；②当t=s或s时，DF将矩形PEQF分成两部分的面积比为1：2.

【解析】试题分析：（1）利用勾股定理先求出AC，根据AQ=AC-CQ即可解决问题；

（2）分两种情形列出方程求解即可；

（3）①分三种情形a、如图1中，当0≤t≤时，重叠部分是四边形PEQF．b、如图2中，当<t≤2时，重叠部分是四边形PNQE．C、如图3中，当2<t≤3时，重叠部分是五边形MNPBQ．分别求解即可；②分两种情形a、如图4中，当DE：DQ=1：2时，DF将矩形PEQF分成两部分的面积比为1：2．b、如图5中，当NE：PN=1：2时，DF将矩形PEQF分成两部分的面积比为1：2．分别列出方程即可解决问题；

试题解析：（1）在Rt△ABC中，∵∠C=90°，AB=10，BC=6，

∴AC===8，

∵CQ=t，

∴AQ=8-t（0≤t≤4）．

（2）①当PQ∥BC时， ，

∴，

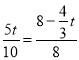∴t=s．

②当PQ∥AB时， ，

∴，

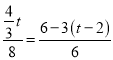∴t=3，

综上所述，t=s或3s时，当PQ与△ABC的一边平行．

（3）①如图1中，a、当0≤t≤时，重叠部分是四边形PEQF．

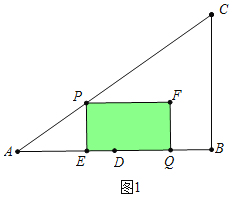
S=PEEQ=3t（8-4t-t）=-16t2+24t．

b、如图2中，当<t≤2时，重叠部分是四边形PNQE．

S=S四边形PEQF-S△PFN=（16t2-24t）-（t-8）（t-8）=t2-t-．

C、如图3中，当2<t≤3时，重叠部分是五边形MNPBQ．

S=S四边形PBQFS△FNM=t[6-3（t-2）]- [t-4（t-2）] [t-4（t-2）]=- t2+30t-24．

综上所述，S=．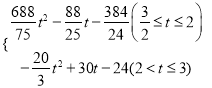

②a、如图4中，当DE：DQ=1：2时，DF将矩形PEQF分成两部分的面积比为1：2．

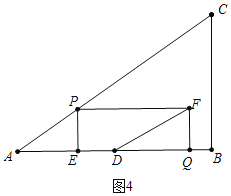
则有（3-3t）：（3-t）=1：2span>，解得t=s，

b、如图5中，当NE：PN=1：2时，DF将矩形PEQF分成两部分的面积比为1：2．

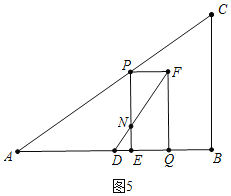
∴DE：DQ=NE：FQ=1：3，

∴（3t-3）：（3-t）=1：3，

解得t=s，

综上所述，当t=s或s时，DF将矩形PEQF分成两部分的面积比为1：2．