【题目】如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
参考答案:
【答案】(1)证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE.
又∵∠A=∠D,∠B=∠C,
∴△ABF≌△DCE(AAS),
∴AB=DC.
(2)解:△OEF为等腰三角形
理由如下:∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF,
∴△OEF为等腰三角形.
【解析】试题分析:(1)根据BE=CF得到BF=CE,又∠A=∠D,∠B=∠C,所以△ABF≌△DCE,根据全等三角形对应边相等即可得证;
(2)根据三角形全等得∠AFB=∠DEC,所以是等腰三角形.
(1)证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE.
又∵∠A=∠D,∠B=∠C,
∴△ABF≌△DCE(AAS),
∴AB=DC.
(2)解:△OEF为等腰三角形
理由如下:∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF,
∴△OEF为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一批衬衣,每件进价为a元,零售价比进价高m%,后因市场变化,该商把零售价调整为原来零售价的n%出售.那么调整后每件衬衣的零售价是( )
A.a(1+m%)(1﹣n%)元
B.am%(1﹣n%)元
C.a(1+m%)n%元
D.a(1+m%n%)元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知n边形的内角和是一个五边形的外角和的2倍,则n=________.
-
科目: 来源: 题型:
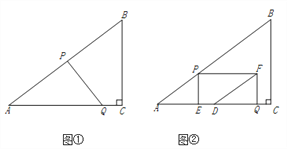
查看答案和解析>>【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6.点P从点A出发,沿折现AB—BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动.点Q从点C出发,沿CA方向以每秒
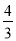 个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.(1)求线段AQ的长.(用含t的代数式表示)
(2)当PQ与△ABC的一边平行时,求t的值
(3)如图②,过点P作PE⊥AC于点E,以PE、QE为邻边作矩形PEQF,点D为AC的中点,连结DF.直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,十位上的数字是2,个位上的数字是x,这个两位数是;
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a2﹣9= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示
(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程.

相关试题

