搜索
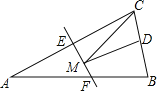
【题目】如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点，若点D为BC边的中点，点M为线段EF上一动点，则
周长的最小值为______．
参考答案：
【答案】10
【解析】
连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AB的垂直平分线可知，点B关于直线EF的对称点为点A，故AD的长为BM+MD的最小值，由此即可得出结论．
解：连接AD，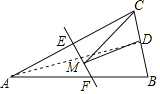
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴S△ABC=
BCAD=×4×AD=16，解得AD=8，
∵EF是线段AB的垂直平分线，
∴点B关于直线EF的对称点为点A，
∴AD的长为CM+MD的最小值，
∴△CDM的周长最短=（CM+MD）+CD=AD+BC=8+×4=8+2=10．
故答案为：10．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用火柴棒按如图方式拼图，第1个图形共用3根火柴棒，第2个图形共用9根火柴棒，第3个图形共用18根火柴棒，……按照这样的方式继续拼图，第n个图形共用_____根火柴棒．（用含n的代数式表示）
-
科目： 来源： 题型：
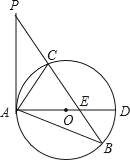
查看答案和解析>>【题目】如图，已知在△ABP中，C是BP边上一点，∠PAC=∠PBA，⊙O是△ABC的外接圆，AD是⊙O的直径，且交BP于点E．
（1）求证：PA是⊙O的切线；
（2）过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AGAB=12，求AC的长；
（3）在满足（2）的条件下，若AF：FD=1：2，GF=1，求⊙O的半径及sin∠ACE的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合与实践
问题情境：在棱长为1的正方体右侧拼搭若干个棱长小于或等于1的其它正方体，使拼成的立体图形为一个长方体．如图1，是两个棱长为1的正方体搭成的长方体，图2是从上面看这个长方体得到的平面图形，它由两个正方形组成．
操作探究：
(1)如图3是在棱长为1的正方体右侧拼搭了4个棱长小于1的正方体形成的长方体，请画出从上面看这个长方体得到的平面图形；
(2)已知一个长方体是按上述方式拼成的，组成它的正方体不超过10个，且若从上面看这个长方体得到的平面图形由4个正方形组成．
请从A，B两题中任选一题作答，我选择 题．
A．请画出从上面看这个长方体得到的平面图形．（请画出所有可能的图形）
B．请画出从上面看这个长方体得到的平面图形．（请画出所有可能的图形，并在所画图形的下方直接写出拼成该长方体所需的正方体的总个数）
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学老师布置了一道思考题“计算（－
）÷（
－
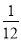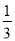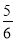）”.小明仔细思考了一番，用了一种不同的方法解决了这个问题：原式的倒数为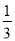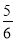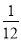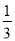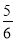（－）÷（－）＝（－）×（－12）＝－4＋10＝6，所以（－）÷（－）＝
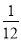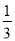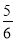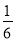.（1）请你通过计算验证小明的解法的正确性.
（2）由此可以得到结论：一个数的倒数的倒数等于_____.
（3）请你运用小明的解法计算：
（－
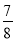）÷（1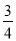
－－
）. -
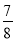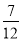科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
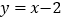与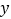
轴交于点C，与
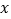轴交于点B，与反比例函数
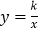的图象在第一象限交于点A，连接OA，且
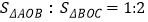．（1）求ΔBOC的面积．
（2）求点A的坐标和反比例函数
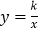的解析式．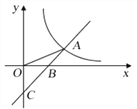 
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店经销一种泰山旅游纪念品，4月份的营业额为2000元，为扩大销售量，5月份该商店对这种纪念品打9折销售，结果销售量增加20件，营业额增加700元．
（1）求该种纪念品4月份的销售价格；
（2）若4月份销售这种纪念品获利800元，5月份销售这种纪念品获利多少元？
相关试题
