搜索
【题目】不论a，b为何实数，a2+b2﹣2a﹣4b+7的值是（ ）
A.总是正数
B.总是负数
C.可以是零
D.可以是正数也可以是负数
参考答案：
【答案】A
【解析】解：∵（a﹣1）2≥0，（b﹣2）2≥0， ∴原式=（a2﹣2a+1）+（b2﹣4b+4）+2=（a﹣1）2+（b﹣2）2+2≥2＞0，
则不论a，b为何实数，a2+b2﹣2a﹣4b+7的值总是正数，
故选A
-
科目： 来源： 题型：
查看答案和解析>>【题目】一元二次方程x2﹣3x＝0的两个根是（ ）
A.x1＝0，x2＝﹣3B.x1＝0，x2＝3C.x1＝1，x2＝3D.x1＝1，x2＝﹣3
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市教研室对2008年嘉兴市中考数学试题的选择题作了错题分析统计，受污损的下表记录了n位同学的错题分布情况：已知这n人中，平均每题有11人答错，同时第6题答错的人数恰好是第5题答错人数的1.5倍，且第2题有80%的同学答对．则第5题有 人答对．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知在平面直角坐标系中有三点A（-2，1）、B（3，1）、C（2，3）．请回答如下问题：
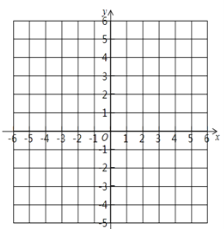
（1）在坐标系内描出点A、B、C的位置，并求△ABC的面积;
（2）在平面直角坐标系中画出△
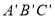,使它与△ABC 关于x轴对称,并写出△ 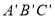三顶点的坐标．（3）若M（x,y）是△ABC内部任意一点，请直接写出这点在△
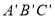内部的对应点M＇的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】中国首款人工智能芯片寒武纪（MLU100），在平衡模式下的等效理论峰值速度达每秒128000000000000次，用科学记数法表示为______次．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市教研室对2008年嘉兴市中考数学试题的选择题作了错题分析统计，受污损的下表记录了n位同学的错题分布情况：已知这n人中，平均每题有11人答错，同时第6题答错的人数恰好是第5题答错人数的1.5倍，且第2题有80%的同学答对．则第5题有 人答对．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若x3m﹣2﹣2yn﹣1=3是二元一次方程，则m= ， n=
相关试题
