【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形. 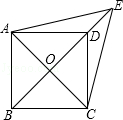
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO.
又∵△ACE是等边三角形,
∴EO⊥AC(三线合一),即AC⊥BD,
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
(2)∵四边形ABCD是平行四边形,
∴AO=CO.
又∵△ACE是等边三角形,
∴EO平分∠AEC(三线合一),
∴∠AED= ![]() ∠AEC=
∠AEC= ![]() ×60°=30°,
×60°=30°,
又∵∠AED=2∠EAD
∴∠EAD=15°,
∴∠ADO=∠DAE+∠DEA=15°+30°=45°(三角形的一个外角等于和它外角不相邻的两内角之和),
∵四边形ABCD是菱形,
∴∠ADC=2∠ADO=90°,
∴平行四边形ABCD是正方形.
【解析】(1)根据对角线互相垂直的平行四边形是菱形.由题意易得△AOE≌△COE,∴∠AOE=∠COE=90°,∴BE⊥AC,∴四边形ABCD是菱形;(2)根据有一个角是90°的菱形是正方形.由题意易得∠ADO=∠DAE+∠DEA=15°+30°=45°,∵四边形ABCD是菱形,∴∠ADC=2∠ADO=90°,∴四边形ABCD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:由面积都是1的小正方格组成的方格平面叫做格点平面.而纵横两组平行线的交点叫做格点.如图1中,有9个格点,如果一个正方形的每个顶点都在格点上,那么这个正方形称为格点正方形.
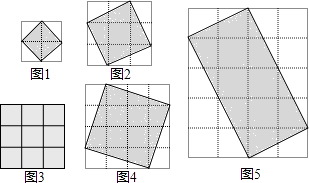
(1)探索发现:按照图形完成下表:格点正方形边上格点数p
格点正方形内格点数q
格点正方形面积S
图1
4
1
2
图2
4
4
图3
4
9
图4
4
关于格点正方形的面积S,从上述表格中你发现了什么规律?
(2)继续猜想:类比格点正方形的概念,如果一个长方形的每个顶点都在格点上,那么这个长方形称为格点长方形,对于格点长方形的面积,你认为也有类似(1)中的规律吗?试以图5中格点长方形为例来说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】北京某天的最高气温是6℃,最低气温是-1℃,则这天的温差是( )
A. -7℃ B. -5℃ C. 5℃ D. 7℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】广州正稳步推进碧道建设,营造“水清岸绿、鱼翔浅底、水草丰美、白鹭成群”的生态廊道,使之成为老百姓美好生活的好去处,到今年底各区完成碧道试点建设的长度分别为(单位:千米):5,5.2,5,5,5,6.4,6,5,6.68,48.4,6.3,这组数据的众数是( )
A. 5B. 5.2C. 6D. 6.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 4m - m = 3 B. a3 - a2 = a C. 2xy - yx = xy D. a2b - ab2 = 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】a,b是有理数,它们在数轴上的对应点的位置如图所示:把a,﹣a,b,﹣b按照从小到大的顺序排列( )
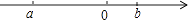
A.﹣b<﹣a<a<b
B.a<﹣b<b<﹣a
C.﹣b<a<﹣a<b
D.a<﹣b<﹣a<b -
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a|=2,|b|=4, ①若
 <0,求a﹣b的值;
<0,求a﹣b的值;
②若|a﹣b|=﹣(a﹣b),求a﹣b的值.
相关试题

