【题目】如图所示,直线y1=![]() x+1与x轴交于点A,与y轴交于点B,与反比例函数y2=
x+1与x轴交于点A,与y轴交于点B,与反比例函数y2=![]() (x>0)的图象交于点C,且AB=BC.
(x>0)的图象交于点C,且AB=BC.
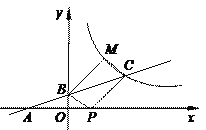
(1) 求点C的坐标和反比例函数y2的解析式;
(2) 点P在x轴上,反比例函数y2图象上存在点M,使得四边形BPCM为平行四边形,求![]() BPCM的面积.
BPCM的面积.
参考答案:
【答案】(1) C(4,2)![]() ;(2)
;(2)![]() .
.
【解析】(1) 过C作CD⊥x轴于D,首先求得直线与x轴和y轴的交点,根据AB=BC可得OA=OD,则B的横坐标即可求得,根据三角形的中位线得CD=2OB,则C的枞坐标可求出,然后利用待定系数法即可求得函数的解析式;
(2) 连结MP与BC交于G,由四边形BPCM为平行四边形,由中点坐标公式可求出点G的坐标,设M(m,![]() ),P(n,0),由中点坐标公式可求得m和n的值,根据S△BPC= S△APC -S△APB求出△BPC的面积,从而可求
),P(n,0),由中点坐标公式可求得m和n的值,根据S△BPC= S△APC -S△APB求出△BPC的面积,从而可求![]() BPCM的面积.
BPCM的面积.
(1)∵直线y1=![]() x+1与x轴交于点A, 与y轴交于点B,
x+1与x轴交于点A, 与y轴交于点B,
∴A(-4,0),B(0,1)
过C作CD⊥x轴于D,
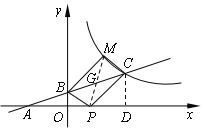
∵AB=BC,
∴OA=OD,
∴OB是△ACD的中位线,
∴D(4,0),C(4,2)
∵点C(4,2)反比例函数y2=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=8,
∴反比例函数y2的解析式y2=![]() ;
;
(2)连结MP与BC交于G,
∵四边形BPCM为平行四边形,
∴G为BC、MP的中点,
由BG=CG,则G(2,![]() ),
),
设M(m,![]() ),P(n,0),
),P(n,0),
由MG=PG,
∴![]() =3,m=
=3,m=![]() ,n=
,n=![]() ,即P(
,即P(![]() ,0),
,0),
S△BPC= S△APC -S△APB= ![]() ,
,
∴![]() BPCM的面积=2 S△BPC=
BPCM的面积=2 S△BPC=![]() ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家5月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形ABCD,点O为AD中点,点E在BD上,连接EO并延长交BC于点F,连接BE,DF.
(1)求证:四边形BEDF是平行四边形;
(2)若AB=3
 ,AD=6,∠BAD=135°,当四边形BEDF为菱形时,求AE的长.
,AD=6,∠BAD=135°,当四边形BEDF为菱形时,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某修理厂需要购进甲、乙两种配件,经调查,每个甲种配件的价格比每个乙种配件的价格少0.4万元,且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同.
(1)求每个甲种配件、每个乙种配件的价格分别为多少万元;
(2)现投入资金80万元,根据维修需要预测,甲种配件要比乙种配件至少要多22件,问乙种配件最多可购买多少件.
-
科目: 来源: 题型:
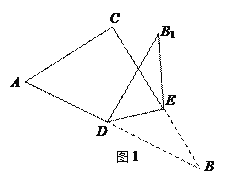
查看答案和解析>>【题目】已知,如图,在Rt△ABC中,∠C=90°,∠A=60°,AC=3,点D为AB的中点,点E为线段BC上的点,连接DE,把△BDE沿着DE翻折得△B1DE.
(1)当A、D、B1、C构成的四边形为平行四边形,求DE的长;
(2)当DB1⊥AC时,求△DE B1和△ABC重叠部分的面积.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,假设航空母舰始终以200千米/时的速度由西向东航行,飞机以800千米/时的速度从舰上起飞,向西航行执行任务,如果飞机在空中最多能连续飞行3个小时,那么它在起飞_____小时后就必须返航,才能安全停在舰上.

相关试题

