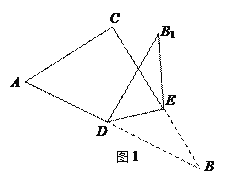
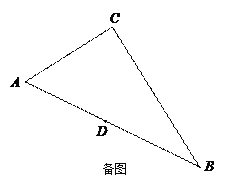
【题目】已知,如图,在Rt△ABC中,∠C=90°,∠A=60°,AC=3,点D为AB的中点,点E为线段BC上的点,连接DE,把△BDE沿着DE翻折得△B1DE.
(1)当A、D、B1、C构成的四边形为平行四边形,求DE的长;
(2)当DB1⊥AC时,求△DE B1和△ABC重叠部分的面积.


参考答案:
【答案】(1)![]() 或3;(2)
或3;(2)![]() .
.
【解析】(1)如图1,由平行四边形的性质得DB1∥AC,且DB1=AC=3,由折叠知BD=DB1= 3,∠BDE=∠EDB1==30°,过E作EH⊥DB于H,则DH=BH=![]() ,在Rt△DEH中,根据勾股定理得DE2=(
,在Rt△DEH中,根据勾股定理得DE2=(![]() DE)2+
DE)2+![]() ,解之可得DE的值;如图2,由平行四边形的性质得B1D∥AC,且B1D=AC=3,又CD=
,解之可得DE的值;如图2,由平行四边形的性质得B1D∥AC,且B1D=AC=3,又CD=![]() AB=3,∠CAB=60°,可证四边形ACDB1为含60°角的菱形,从而∠E B1D=∠C B1D =30°,即E与C重合,DE的长即是CD的长.
AB=3,∠CAB=60°,可证四边形ACDB1为含60°角的菱形,从而∠E B1D=∠C B1D =30°,即E与C重合,DE的长即是CD的长.
(2)设B1D、B1E分别与AC交于P、Q,在Rt△ADP中,求出AP和DP的长,在Rt△B1PQ中,求出B 1P和PQ的长,然后根据△DE B1和△ABC重叠部分的面积=S△B1DE- S△B1PQ计算即可.
(1)如图1,若四边形为ACB1D的平行四边形,则有DB1∥AC,且DB1=AC=3,
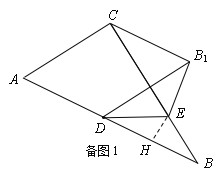
由题意,∠B=30°,∠BDE=∠EDB1=30°,
∴DE=BE,
在Rt△ABC中,∠A=60°,AC=3,∴AB=6,BD=3,
过E作EH⊥DB于H,则DH=BH=![]() ,
,
在Rt△DEH中,EH=![]() DE,DH=
DE,DH=![]() ,
,
∴DE2=(![]() DE)2+
DE)2+![]() ,
,
∴DE=![]() ;
;
如图2,若四边形为ACDB1的平行四边形,则有,B1D∥AC,且B1D=AC=3,

∵CD=![]() AB=3,∠CAB=60°,
AB=3,∠CAB=60°,
∴四边形ACDB1为含60°角的菱形,
∵∠E B1D=∠C B1D =30°,
∴E与C重合,
∴DE=CD=3;
综上,DE=![]() 或3,
或3,
(2)当DB1⊥AC时(如图3),设B1D、B1E分别与AC交于P、Q,
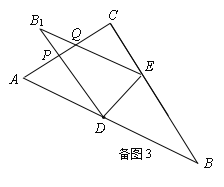
则:Rt△ADP中,∠A=60°,AD=3,
∴AP=![]() ,DP=
,DP=![]()
![]() ,
,
Rt△B1PQ中,∠B 1=∠B=30°,B 1P=3-![]()
![]() ,
,
∴PQ=![]() -
-![]() ,
,
∴S△B1PQ=![]() ×B 1P
×B 1P![]() PQ=
PQ=![]() ×(3-
×(3-![]()
![]() )(
)(![]() -
-![]() )=
)=![]() -
-![]() ,
,
又S△B1DE==![]() ×DB 1
×DB 1![]() PC=
PC=![]() ×3×
×3×![]() =
=![]() ,
,
∴△DE B1和△ABC重叠部分的面积=![]() -
-![]() +
+![]() =
=![]() -
-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形ABCD,点O为AD中点,点E在BD上,连接EO并延长交BC于点F,连接BE,DF.
(1)求证:四边形BEDF是平行四边形;
(2)若AB=3
 ,AD=6,∠BAD=135°,当四边形BEDF为菱形时,求AE的长.
,AD=6,∠BAD=135°,当四边形BEDF为菱形时,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线y1=
 x+1与x轴交于点A,与y轴交于点B,与反比例函数y2=
x+1与x轴交于点A,与y轴交于点B,与反比例函数y2= (x>0)的图象交于点C,且AB=BC.
(x>0)的图象交于点C,且AB=BC.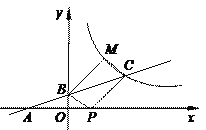
(1) 求点C的坐标和反比例函数y2的解析式;
(2) 点P在x轴上,反比例函数y2图象上存在点M,使得四边形BPCM为平行四边形,求
 BPCM的面积.
BPCM的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某修理厂需要购进甲、乙两种配件,经调查,每个甲种配件的价格比每个乙种配件的价格少0.4万元,且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同.
(1)求每个甲种配件、每个乙种配件的价格分别为多少万元;
(2)现投入资金80万元,根据维修需要预测,甲种配件要比乙种配件至少要多22件,问乙种配件最多可购买多少件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,假设航空母舰始终以200千米/时的速度由西向东航行,飞机以800千米/时的速度从舰上起飞,向西航行执行任务,如果飞机在空中最多能连续飞行3个小时,那么它在起飞_____小时后就必须返航,才能安全停在舰上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)来表示,例如f(x)=x2+3x﹣5,把x=某数时多项式的值用f(某数)来表示,例如x=1时多项式x2+3x﹣5的值记为f(1)=12+3×1﹣5=﹣1.
(1)已知g(x)=﹣2x2﹣3x+1,分别求出g(﹣1)和g(﹣2)的值.
(2)已知h(x)=ax3+2x2﹣x﹣14,
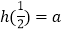 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )

A. 6
 B. 6C. 3
B. 6C. 3 D. 3+3
D. 3+3
相关试题

