【题目】如图一,矩形ABCD中,AB=5cm,BC=4cm,E是BC上一点,将△CDE沿DE折叠,使点C落在AB上一点F处,连结DF、EF. 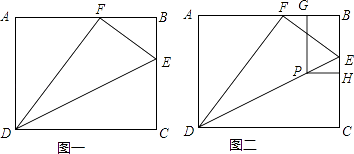
(1)求BE的长度;
(2)设点P、H、G分别在线段DE、BC、BA上,当BP=CP且四边形BGPH为矩形时,请说明矩形BGPH的长宽比为2:1,并求PE的长.(如图二)
参考答案:
【答案】
(1)解:如图一,
在矩形ABCD中,AD=BC=4,CD=AB=5,∠A=90°,
由折叠可得:DF=DC=5,CE=CF,
∴直角三角形ADF中,AF= ![]() =3,
=3,
∴BF=5=3=2,
设BE=x,则CE=FE=4﹣x,
在Rt△BEF中,22+x2=(4﹣x)2,
解得x=1.5,
即BE=1.5
(2)解:如图二,当BP=CP,且四边形BGPH为矩形时,点P在BC的垂直平分线上,
即PH垂直平分BC,
∴BH=CH= ![]() BC=2,①
BC=2,①
又∵BE=1.5,
∴EH=0.5,EC=2.5
∵PH∥DC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]()
解得PH=1,②
∴由①②得:矩形BGPH的长宽比为2:1,
在Rt△PEH中,PE= ![]() =
= ![]() =
= ![]()
【解析】(1)先根据矩形性质以及折叠变换,运用勾股定理求得AF、BF的长,再设BE=x,在Rt△BEF中运用勾股定理列出方程,求得x的值.(2)先判断PH垂直平分BC,求得矩形中BH的长,再根据平行线分线段成比例定理,求得PH的长,进而得出矩形BGPH的长宽比为2:1,最后根据勾股定理求得PE的长.
【考点精析】利用勾股定理的概念和矩形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2s,方差如下表:
选手
甲
乙
丙
丁
方差(s2)
0.020
0.019
0.021
0.022
则这四人中发挥最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,设安排x名工人生产螺钉,则下面所列方程正确的是( )
A.1000(26﹣x)=800x
B.1000(13﹣x)=800x
C.1000(26﹣x)=2×800x
D.2×1000(26﹣x)=800x -
科目: 来源: 题型:
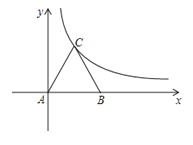
查看答案和解析>>【题目】如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),反比例函数的图象经过点C.
(1)求点C的坐标及反比例函数的解析式.
(2)将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现在网购已成为人们的一种消费方式,在2015年的“双11”促销活动中天猫和淘宝的支付交易额突破57000000000元,将数字57000000000用科学记数法表示为元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)16÷(﹣23)﹣(﹣
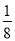 )×(﹣4)
)×(﹣4)(2)﹣4﹣(﹣
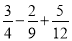 )÷
)÷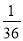
(3)﹣14﹣[2﹣(﹣3)2]÷(﹣
 )3.
)3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.

(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
相关试题

