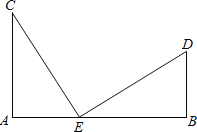
【题目】如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,
(1)△AEC≌△BDE吗,请说明理由
(2)试猜想线段CE与DE大小与位置关系,说明理由.
参考答案:
【答案】见解析
【解析】先利用HL判定△AEC≌△BDE,从而得出全等三角形的对应角相等,再利用角与角之间的关系,可以得到线段CE与DE的大小与位置关系为相等且垂直.
解:(1)△AEC≌△BDE,理由为:
因为AC⊥AB,DB⊥AB,所以∠CAE=∠DBE=90°,
又因为AC=BE,AE=BD,所以△AEC≌△BDE.
(2)CE=DE,CE⊥DE,理由为:
由(1)可知,△AEC≌△BDE,所以CE=DE,∠C=∠DEB,
又因为在Rt△AEC中,∠C+∠CEA=90°,
所以∠DEB+∠CEA=90°,所以∠CED=90°,
所以CE⊥DE.
“点睛”本题考查了全等三角形的判定和性质,垂直的定义、平角的定义,熟练掌握全等三角形的判定定理是解题的关键.
-
科目: 来源: 题型:
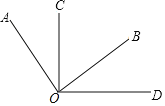
查看答案和解析>>【题目】如图,∠AOB=∠COD=90
(1)若∠BOC=32,∠AOD的度数是多少?
(2)若∠AOD=132,∠BOC的度数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-2,3)关于x轴的对称点的坐标为( )
A.(2,3)B.(-2,-3)C.(2,-3)D.(-3,2)
-
科目: 来源: 题型:
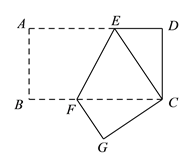
查看答案和解析>>【题目】已知将一矩形纸片ABCD折叠,使顶点A与C重合,折痕为EF.
(1)求证:CE=CF;
(2)若AB =8 cm,BC=16 cm,连接AF,写出求四边形AFCE面积的思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2开始,连续的偶数相加,它们和的情况如下表:

(1)如果n=8时,那么S的值为________;
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n=_________;
(3)根据上题的规律计算102+104+106+…+2006的值(要有计算过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b中,x取不同值时,y对应的值列表如下:
x
…
-m2-1
2
3
…
y
…
-1
0
n2+1
…
则不等式kx+b>0(其中k,b,m,n为常数)的解集为( )
A.x>2
B.x>3
C.x<2
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】无锡地铁3号线预计全长约42500米,将42500用科学记数法表示为 .
相关试题

