【题目】用配方法解关于x的一元二次方程ax2+bx+c=0.
参考答案:
【答案】当b2﹣4ac>0时,x1=![]() ,x2=
,x2=![]() ,
,
当b2﹣4ac=0时,解得:x1=x2=﹣![]() ;
;
当b2﹣4ac<0时,原方程无实数根.
【解析】试题分析:
先把原方程的两边都除以二次项的系数a,化为二次项系数是1的一元二次方程,常数项移到方程的右边,方程两边都加上一次项系数的一半的平方,使左边配成一个完全平方式,再用直接开平方法求解,注意讨论b2-4ac的符号.
试题解析:
解:∵关于x的方程ax2+bx+c=0是一元二次方程,∴a≠0.
∴由原方程,得x2+![]() x=﹣
x=﹣![]() ,
,
等式的两边都加上![]() ,得x2+
,得x2+![]() x+
x+![]() =﹣
=﹣![]() +
+![]() ,
,
配方,得(x+![]() )2=﹣
)2=﹣![]() ,
,
当b2﹣4ac>0时,
开方,得:x+![]() =±
=±![]() ,
,
解得x1=![]() ,x2=
,x2=![]() ,
,
当b2﹣4ac=0时,解得:x1=x2=﹣![]() ;
;
当b2﹣4ac<0时,原方程无实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
 的图象如图所示,则以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(-1,a),点B(2,b)在图象上,则a <b;④若点P(x,y)在图象上,则点P1(-x,y)也在图象上.其中正确的个数为( )
的图象如图所示,则以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(-1,a),点B(2,b)在图象上,则a <b;④若点P(x,y)在图象上,则点P1(-x,y)也在图象上.其中正确的个数为( )
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点P(1,4),Q(m,n)在函数y=
 (x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C,D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C,D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
A. 减小 B. 增大 C. 先减小后增大 D. 先增大后减小
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数
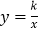 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数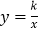 的图象于点M,△AOM的面积为3.
的图象于点M,△AOM的面积为3.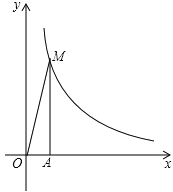
(1)求反比例函数的解析式;
(2)设点B的坐标为(t,0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数
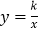 的图象上,求t的值.
的图象上,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:如图,已知∠B=∠CGF,∠DGF=∠F,试说明∠B+∠F=180°.
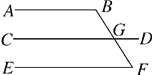
解:∵∠B=________(已知),
∴AB∥CD(______________________).
∵∠DGF=____________(已知),
∴CD∥EF(____________________).
∴AB∥EF(___________________).
∴∠B+______=180°(__________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知BC∥OA,∠B=∠A=100°,试回答下列问题:

(1)如图①所示,试说明OB∥AC;
(2)如图②,若点E,F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于________(在横线上填上答案即可);
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB∶∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(4)在(3)的条件下,在平行移动AC的过程中,若使∠OEB=∠OCA,此时∠OCA的度数等于________(在横线上填上答案即可).
相关试题

