【题目】某校数学研究小组在研究有关二次函数及其图象性质时,发现了一个重要结论:抛物线y=ax2+2x+3(a≠0),当实数a变化时,它们的顶点都在某条直线上.
(1)请你协助探求出这条直线的表达式;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它吗?并说明理由.
参考答案:
【答案】(1)y=x+3;(2)见解析
【解析】试题分析:(1)可以取a=1或-1,分别求出抛物线的顶点坐标,运用“两点法”求直线解析式;
(2)运用顶点坐标公式,先表示抛物线的顶点坐标,再根据a的取值范围进行判断.
试题解析:解:(1)当a=1时,y=x2+2x+3的顶点是(﹣1,2).
当a=﹣1时,y=﹣x2+2x+3的顶点是(1,4).
设直线的表达式为y=kx+b,则:![]() ,解得:
,解得:![]() ,
,
∴所求直线的表达式为y=x+3;
(2)抛物线y=ax2+2x+3的顶点是(![]() ,
,![]() ),而
),而![]() ≠0,
≠0,![]() ≠3,∴直线y=x+3一个点(0,3)不是该抛物线的顶点.
≠3,∴直线y=x+3一个点(0,3)不是该抛物线的顶点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,x=
 是该抛物线的对称轴,根据图中所提供的信息,请写出有关a,b,c的四条结论,并简要说明理由.
是该抛物线的对称轴,根据图中所提供的信息,请写出有关a,b,c的四条结论,并简要说明理由.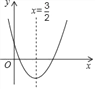
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的边长为2,∠B=60°,点P、Q分别是边BC、CD上的动点(不与端点重合),且BP=CQ.

(1)图中除了△ABC与△ADC外,还有哪些三角形全等,请写出来;
(2)点P、Q在运动过程中,四边形APCQ的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
(3)当点P在什么位置时,△PCQ的面积最大,并请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 轴于点(1,0),直线
轴于点(1,0),直线 轴于点(2,0),直线
轴于点(2,0),直线 轴于点(3,0),…,直线
轴于点(3,0),…,直线 轴于点(n,0)。函数
轴于点(n,0)。函数 的图象与直线
的图象与直线 分别交于点
分别交于点 ;函数
;函数 的图象与直线
的图象与直线 分别交于点
分别交于点 。如果
。如果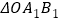 的面积记作
的面积记作 ,四边形
,四边形 的面积记作
的面积记作 ,四边形
,四边形 的面积记作
的面积记作 ,…,四边形
,…,四边形 的面积记作
的面积记作 ,那么
,那么 _____________.
_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1与直线l2:y=
 x+3平行,直线l1与x轴的交点的坐标为A(2,0),求:
x+3平行,直线l1与x轴的交点的坐标为A(2,0),求:(1)直线l1的表达式.
(2)直线l1与坐标轴围成的三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B分别是x轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,3),直线PB交y轴于点D,△AOP的面积为12;
(1)求△COP的面积;
(2)求点A的坐标及p的值;
(3)若△BOP与△DOP的面积相等,求直线BD的函数解析式.

-
科目: 来源: 题型:
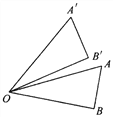
查看答案和解析>>【题目】如图,Rt△AOB绕着一点旋转到△A′OB′的位置,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段和角.已知∠AOB=30°,∠AOB′=10°,那么点B的对应点是点______;线段OB的对应线段是线段_____;∠A的对应角是______;旋转中心是点_______;旋转的角度是______度.
相关试题

