【题目】(1)如图![]() 示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
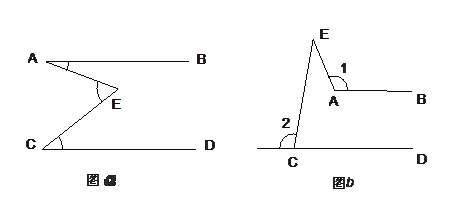
(2)现在如图b示,仍有AB∥CD,但点E在AB与CD的上方,①请尝试探索∠1,∠2,∠E三者的数量关系. ②请说明理由.
参考答案:
【答案】(1)证明见解析(2)∠1+∠2-∠E=180°
【解析】
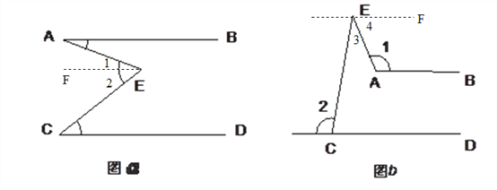
试题(1)过点E作EF∥AB,由两直线平行,内错角相等,得到∠A=∠1.
由平行的传递性得到EF // CD,再由平行线的性质得到∠2=∠C,由角的和差即可得到结论;
(2)过点E作EF∥AB,类似可得到结论.
试题解析:解:(1)过点E作EF∥AB,∴∠A=∠1(两直线平行,内错角相等).
∵AB // CD(已知),∴EF // CD(平行的传递性),∴∠2=∠C(两直线平行,内错角相等).
∵∠AEC=∠1+∠2(图上可知),∴∠AEC=∠A+∠C(等量代换) ;
(2)∠1+∠2-∠E=180°.理由如下:
过点E作EF∥AB,∴∠4+∠1=180°(两直线平行,同旁内角互补).
∵AB // CD(已知),∴EF // CD(平行的传递性),∴∠FEC=∠2(两直线平行,内错角相等),即∠3+∠4=∠2,∴∠4=∠2-∠3(等式性质),∴∠2-∠3+∠1=180°(等量代换),
即∠1+∠2-∠AEC=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在等边三角形ABC中,
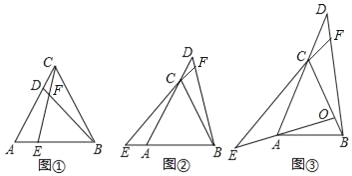
①如图①,D,E分别是边AC,AB上的点且AE=CD,BD与EC交于点F,则∠BFE的度数是 度;
②如图②,D,E分别是边AC,BA延长线上的点且AE=CD,BD与EC的延长线交于点F,此时∠BFE的度数是 度;
(2)如图③,在△ABC中,AC=BC,∠ACB是锐角,点O是AC边的垂直平分线与BC的交点,点D,E分别在AC,OA的延长线上,AE=CD,BD与EC的延长线交于点F,若∠ACB=α,求∠BFE的大小.(用含α的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=﹣(x﹣2)2+
 的图象与x轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有个(提示:必要时可利用下面的备用图画出图象来分析).
的图象与x轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有个(提示:必要时可利用下面的备用图画出图象来分析). 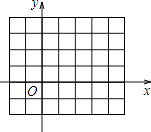
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰△ABC的顶角∠A=36°(如图).
(1)作底角∠ABC的平分线BD,交AC于点D(用尺规作图,不写作法,但保留作图痕迹,然后用墨水笔加墨);
(2)通过计算说明△ABD和△BDC都是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】(c2012防城港)某奶品生产企业,2010年对铁锌牛奶、酸牛奶、纯牛奶三个品种的生产情况进行了统计,绘制了图1、2的统计图,请根据图中信息解答下列问题:

(1)酸牛奶生产了多少万吨?把图1补充完整;酸牛奶在图2所对应的圆心角是多少度?
(2)由于市场不断需求,据统计,2011年的生产量比2010年增长20%,按照这样的增长速度,请你估算2012年酸牛奶的生产量是多少万吨? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
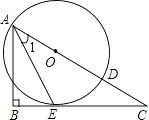
(1)求证:AE平分∠CAB;
(2)探求图中∠1与∠C的数量关系,并求当AE=EC时tanC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在实践中学习:
(1)如图1所示:已知AB∥CD,∠ABD=115°,根据 可得出:∠BDC的度数是 .
(2)如图2所示:已知AB∥CD,∠ABC=25°,∠EDC=40°,求∠BED的度数.(3)如图3所示:已知MA∥NC,试确定∠A、∠B、∠C和∠E、∠F的关系,并说明理由.
(4)如图4所示:已知AB∥CD,∠ABE=α,∠FCD=β,∠CFE=γ,且BE⊥EF,试确定α、β、γ的关系,请说明理由.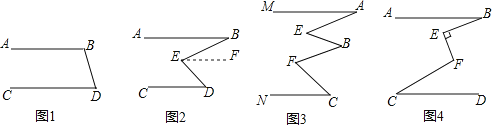
相关试题

