Question

【题目】如图，在平面直角坐标系中，△AOP为等边三角形，A（0，5），点B为y轴正半轴上一动点，以BP为边作如图所示等边△PBC．CA的延长线交x轴交于E．

（1）求证：OB＝AC；

（2）求∠CAP的度数；

（3）当B点运动时，AE的长度是否发生变化？若不发生变化，请求出AE的值，若发生变化，请说明理由．

Answer 1

【答案】（1）见解析；（2）∠CAP＝60°；（3）不发生变化，理由见解析．

【解析】

（1）利用等边三角形的性质可知∠OPB＝∠APC，然后可证△PBO≌△PCA，则可证OB＝AC

（2）由全等三角形的性质可知∠PBO＝∠PCA，根据∠BAC＝∠BPC＝60°及平角的定义即可求出∠CAP的度数.

（3）根据∠EAO＝∠BAC＝60°可知∠AEO，从而可知AE＝2AO，所以AE的长度不发生变化.

（1）证明：∵△BPC和△AOP是等边三角形，

∴OP＝AP，BP＝PC，∠APO＝60°，∠CPB＝60°，

∴∠APO+∠APB＝∠BPC+∠APB，即∠OPB＝∠APC，

在△PBO和△PCA中，

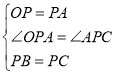
∴△PBO≌△PCA （SAS），

∴OB＝AC；

（2）解：由（1）知，△PBO≌△PCA，

∴∠PBO＝∠PCA，

∴∠BAC＝∠BPC＝60°，

又∠OAP＝60°，

∴∠CAP＝60°；

（3）解：当B点运动时，AE的长度不发生变化，

理由如下：∵∠EAO＝∠BAC＝60°，∠AOE＝90°，

∴∠AEO＝30°，

∴AE＝2AO＝2，

即当B点运动时，AE的长度不发生变化．