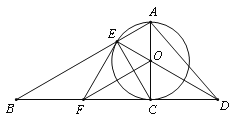
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,作OF∥AB交BC于点F,连接EF.
(1)求证:OF⊥CE
(2)求证:EF是⊙O的切线;
(3)若![]() O的半径为3,∠EAC=60°,求AD的长.
O的半径为3,∠EAC=60°,求AD的长.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)AD=![]() .
.
【解析】试题分析: (1)根据直径所对的圆周角为直角可得CE⊥AE。根据中位线的定义可得OF为△ABC的中位线,由中位线的性质,OF//AB。根据平行线的性质,所以CE⊥OF。(2)在(1)的条件下,又有EO=OC,根据中垂线的性质,可得OF垂直平分CE,根据垂直平分线上的点到的线段两端点的距离相等,所以FC=FE,根据边边边定理可判定△OCF△OEF,根据全等三角形的性质可得OE⊥EF.根据切线性质,所以EF是⊙O的切线.
(3)根据等边三角形的判定可得△AEO为等边三角形,由等边三角形性质可得∠EOA=60°.由对顶角相等可得∠COD=∠EOA=60°.在Rt△OCD中,根据三角函数关系可得,CD=![]() .在Rt△ACD中,根据勾股定理可得AD的长.
.在Rt△ACD中,根据勾股定理可得AD的长.
试题解析:
解:如图,
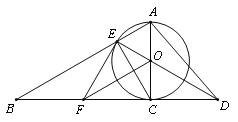
(1)证明:∵AC是⊙O的直径,
∴CE⊥AE
∵OF∥AB
∴OF⊥CE;
(2)证明:∵OF⊥CE
∴OF所在直线垂直平分CE,
∴FC=FE
∴∠FCE=∠FEC,
又∵OE=OC,
∠OEC=∠OCE,
∵∠ACB=90°,
即∠OCE+∠FCE=90°,
∴∠OEC+∠FEC=90°,
即∠FEO=90°,
∴FE为![]() O的切线.
O的切线.
(3)∵![]() O的半径为3,
O的半径为3,
∴AO=CO=EO=3.
∵∠EAC=60°,OA=OE,∴△AEO为等边三角形,
∴∠EOA=60°,
∴∠COD=∠EOA=60°.
∵在Rt△OCD中,∠COD=60°,OC=3,
∴CD=![]() .
.
∵在Rt△ACD中,∠ACD=90°,AC=6,
∴AD=![]() =
=![]() =
=![]() =
=![]() .
.
点睛: 本题考查了切线的判定和性质,三角形的中位线的性质,勾股定理,线段垂直平分线的性质,直角三角形的性质,熟练掌握定理是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料,并解答相应的问题:
幻方
将若干个数组成一个正方形数阵,若任意一行,一列及对角线上的数字之和都相等,则称具有这种性质的数字方阵为“幻方”.中国古代称“幻方”为“河图”、“洛书”等.例如,下面是三个三阶幻方,是将数字1,2,3,4,5,6,7,8,9填入到3×3的方格中得到的,其每行、每列、每条对角线上的三个数之和相等.

(1)设下面的三阶幻方中间的数字是x(其中x为正整数),请用含x的代数式将下面的幻方填充完整.
x+3
x﹣4
x﹣2
x
x﹣1
x﹣3
(2)若设(1)题幻方中9个数的和为S,则S与中间的数字x之间的数量关系为 .
(3)请在下面的A、B两题中任选一题作答,我选择 .
现要用9个数3,4,5,6,7,8,9,10,11构造一个三阶幻方.
A、幻方最中间的数字应等于 .
B、请将构造的幻方填写在下面3×3的方格中.

-
科目: 来源: 题型:
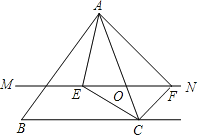
查看答案和解析>>【题目】如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF.那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正在建设的成都第二绕城高速全长超过220公里,串起我市二、三圈层以及周边的广汉、简阳等地,总投资达290亿元,用科学计数法表示290亿元应为( )
A. 290×
 B. 290×
B. 290×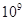
C. 2.90×
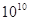 D. 2.90×
D. 2.90×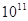
-
科目: 来源: 题型:
查看答案和解析>>【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期
一
二
三
四
五
六
日
增减
-5
+7
-3
+4
+10
-9
-25
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,則四辺形ABFD的周长为( )

A. 16cmB. 18cmC. 20cmD. 22cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个质点在第一象限及
 轴、
轴、 轴上运动, 在第一秒钟,它从原点运动到
轴上运动, 在第一秒钟,它从原点运动到 ,然后接着按图中箭头所示方向运动,且每秒移动一个单位,那么第
,然后接着按图中箭头所示方向运动,且每秒移动一个单位,那么第 秒时质点所在位置的坐标是( )
秒时质点所在位置的坐标是( )
A.
 B.
B.  C.
C.  D.
D. 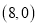
相关试题

