Question

【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：

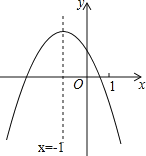
①b2﹣4ac＞0；

②4a+c＞2b；

③（a+c）2＞b2；

④x（ax+b）≤a﹣b．

其中正确结论的是 ．（请把正确结论的序号都填在横线上）

Answer 1

【答案】①②④

【解析】

试题分析：①根据抛物线与x轴有两个交点进行判断即可；

②根据当x=﹣2时，y＞0判断即可；

③根据x=﹣1时，y＞0可知a﹣b+c＞0，判断即可；

④根据x=﹣1时，y有最大值a﹣b+c判断即可．

解：①∵抛物线与x轴由两个交点，

∴b2﹣4ac＞0，

①正确；

②由图象可知，当x=﹣2时，y＞0，

即4a﹣2b+c＞0，

∴4a+c＞2b，

②正确；

③∵x=﹣1时，y＞0，

∴a﹣b+c＞0，

∴a+c＞b，

∵a+b+c＜0，∴a+c＜﹣b，

∴（a+c）2＜b2，

③错误；

④∵x=﹣1时，y有最大值a﹣b+c，

∴ax2+bx+c≤a﹣b+c，

∴x（ax+b）≤a﹣b，

④正确．

故答案为：①②④．