Question

【题目】如图，四边形ABCD是矩形，直线l垂直平分线段AC，垂足为O，直线l分别与线段AD、CB的延长线交于点E、F．
（1）△ABC与△FOA相似吗？为什么？
（2）试判定四边形AFCE的形状，并说明理由．

Answer 1

【答案】
（1）解：∴△ABC∽△FOA，理由如下：

∵直线l垂直平分线段AC，

∴∠AFO=∠CFO，

∵∠CFO+∠FCO=∠CAB+∠FCO=90°，

∴∠AFO=∠CAB，

∵∠AOF=∠CBA=90°，

∴△ABC∽△FOA

（2）解：四边形AFCE是菱形，理由如下：

由（1）知△ABC∽△FOA，

∴∠ACB=∠FAC，

∵AD∥BC，

∴∠ACB=∠EAC，

∴∠FAC=∠EAC，

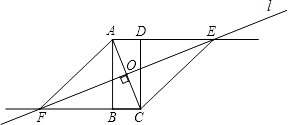
在△AOF与△AOE中，

，

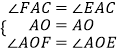∴△AOF≌△AOE（ASA），

∴AE=AF，FO=EO．

∵四边形ABCD是矩形，

∴四边形AFCE是平行四边形，

∴四边形AFCE是菱形．

【解析】（1）根据角平分线的定义，同角的余角相等可知∠AFO=∠CAB，根据垂直的定义，矩形的性质可知∠ABC=∠FOA，由相似三角形的判定可证△ABC与△FOA相似；（2）先证明四边形AFCE是平行四边形，再根据对角线互相垂直平分的平行四边形是菱形作出判断．
【考点精析】根据题目的已知条件，利用线段垂直平分线的性质和菱形的判定方法的相关知识可以得到问题的答案，需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形．