【题目】如图,边长为2的正方形ABCD内接于⊙O,点E是 ![]() 上一点(不与A、B重合),点F是
上一点(不与A、B重合),点F是 ![]() 上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:
上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:
① ![]() =
= ![]() ;
;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④若BG=1﹣ ![]() ,则BG,GE,
,则BG,GE, ![]() 围成的面积是
围成的面积是 ![]() +
+ ![]() .
.
其中正确的是(把所有正确结论的序号都填上)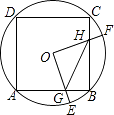
参考答案:
【答案】①②
【解析】如图所示,连接OC、OB、CF、BE.
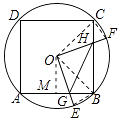
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
∴ ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ;故①正确,
;故①正确,
在△BOG与△COH中,
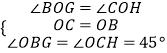 ,
,
∴△BOG≌△COH(ASA),
∴OG=OH,
∵∠HOG=90°
∴△OGH是等腰直角三角形,②正确,
∴S△OBG=S△OCH,
∴S四边形OGBH=S△BOC= ![]() S正方形ABCD=定值,故③错误;
S正方形ABCD=定值,故③错误;
作OM⊥AB于M,则OM=BM= ![]() AB=1,OB=
AB=1,OB= ![]() OM=
OM= ![]() ,
,
∴GM= ![]() ,
,
∴tan∠GOM= ![]() =
= ![]() ,
,
∴∠GOM=30°,
∵∠BOM=45°,
∴∠BOG=45°﹣30°=15°,
∴扇形BOE的面积= ![]() =
= ![]() ,
,
∵BG=1﹣ ![]() ,
,
∴AG=1+ ![]() ,
,
过G作GP⊥BO于P,
∴PG=PB= ![]() ﹣
﹣ ![]() ,
,
∴△OBG的面积= ![]() ×
× ![]() ×(
×( ![]() ﹣
﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() ,
,
∴BG,GE, ![]() 围成的面积=扇形BOE的面积﹣△BOG的面积=
围成的面积=扇形BOE的面积﹣△BOG的面积= ![]() ﹣
﹣ ![]() +
+ ![]() ,故④错误.
,故④错误.
所以答案是:①②.
【考点精析】根据题目的已知条件,利用正多边形和圆和扇形面积计算公式的相关知识可以得到问题的答案,需要掌握圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知2x﹣1的平方根是±6,2x+y﹣1的算术平方根是5,求2x﹣3y+11的立方根.
(2)已知x是1的平方根,求代数式(x2017﹣1)(x2018﹣712)(x2019+1)(x2020+712)+1000x的立方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝广西壮族自治区成立60周年,某校团委组织开展了以“壮美广西”为主题的演讲比赛,并购买同一品牌的壮锦和画册作为奖励.已知购买一副壮锦比购买一副画册多用
 元,若用
元,若用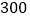 元购买壮锦和
元购买壮锦和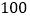 元购买画册,则购买壮锦的数量是购买画册数量的
元购买画册,则购买壮锦的数量是购买画册数量的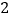 倍.
倍.(1)求购买该品牌的每副画册和每副壮锦各需要多少元?
(2)经洽商,学校团委获得了购买一副该品牌的壮锦赠送一副该品牌的画册的优惠.如果本次活动需要的画册数量是壮锦数量的
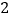 倍少
倍少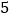 副,且总费用不超过
副,且总费用不超过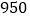 元,那么学校团委最多可购买多少副壮锦?
元,那么学校团委最多可购买多少副壮锦? -
科目: 来源: 题型:
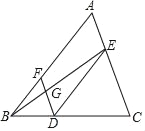
查看答案和解析>>【题目】完成下面的证明:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED( )
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD( )
∴DF∥AE( )
∴∠EGF+∠AEG=180°( )
-
科目: 来源: 题型:
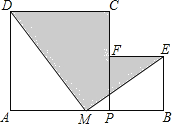
查看答案和解析>>【题目】如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连结MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下面各题
(1)计算:﹣22+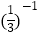 ﹣2cos60°+|﹣3|;
﹣2cos60°+|﹣3|;
(2)解不等式组: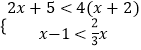 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图所示,(单位:cm)

(1)列出方程(组),求出图甲中a与b的值.
(2)在试生产阶段,若将m张标准板材用裁法一裁剪,n张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙横式无盖礼品盒.
①两种裁法共产生A型板材 张,B型板材 张(用m、n的代数式表示);
②当30≤m≤40时,所裁得的A型板材和B型板材恰好用完,做成的横式无盖礼品盒可能是 个.(在横线上直接写出所有可能答案,无需书写过程)
相关试题

