【题目】如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
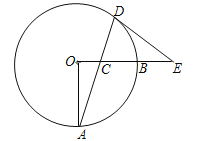
(1)求证:∠ECD=∠EDC;
(2)若tanA=![]() ,求DE长;
,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
参考答案:
【答案】(1)证明见解析;
(2)DE的长为15;
(3)弦AD在圆内扫过的面积为![]()
【解析】试题分析:(1)连结OD,已知DE是⊙O的切线,根据切线的性质可得∠EDC+∠ODA=90°,已知 OA⊥OB,可得∠ACO+∠A=90°,因OA=OD,根据等腰三角形的性质可得∠ODA=∠A,即可得∠EDC=∠ACO,因∠ECD=∠ACO,即可得∠ECD=∠EDC.(2)因为tanA=![]() ,即可得
,即可得![]() ,求得OC=2, 设DE=x,可得CE=x,所以OE=2+x,在Rt△ODE中,根据勾股定理可得OD2+DE2=OE2, 即可得82+x 2=(2+x)2,解得x=15,所以DE=CE=15. (3)过点D作AO的垂线,交AO的延长于F,当
,求得OC=2, 设DE=x,可得CE=x,所以OE=2+x,在Rt△ODE中,根据勾股定理可得OD2+DE2=OE2, 即可得82+x 2=(2+x)2,解得x=15,所以DE=CE=15. (3)过点D作AO的垂线,交AO的延长于F,当![]() 时,
时, ![]() ,DF=4,求得
,DF=4,求得![]() 的面积,当
的面积,当![]() 时,
时, ![]() ,DF=4
,DF=4![]() ,求得
,求得![]() ,即可求得弦AD在圆内扫过的面积.
,即可求得弦AD在圆内扫过的面积.
试题解析:
(1)证明:连结OD,
∵DE是⊙O的切线,∴∠EDC+∠ODA=900,
又∵OA⊥OB,∴∠ACO+∠A=900,
∵OA=OD,∴∠ODA=∠A,∴∠EDC=∠ACO,
又∵∠ECD=∠ACO,∴∠ECD=∠EDC.
(2)解:∵tanA=![]() ,∴
,∴![]() ,∴OC=2,
,∴OC=2,
设DE=x,∵∠ECD=∠EDC,∴CE=x,∴OE=2+x.
∴∠ODE=900,∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,∴DE=CE=15.
(3)解:过点D作AO的垂线,交AO的延长于F,
当![]() 时,
时, ![]() ,DF=4,
,DF=4,
![]()
当![]() 时,
时, ![]() ,DF=4
,DF=4![]() ,
,
![]() ,
,
![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a+2a=3a2
B.aa2=a3
C.(2a)2=2a2
D.(﹣a2)3=a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】探究:如图1 ,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数
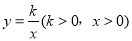 的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).(1)若
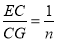 ,请用含n的代数式表示
,请用含n的代数式表示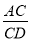 ;
;(2)求证:
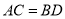 ;
;应用:如图2,直线l与坐标轴的正半轴分别交于点A,B两点,与反比例函数
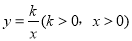 的图象交于点C,D两点(点C在点D的左边),已知
的图象交于点C,D两点(点C在点D的左边),已知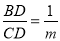 ,△OBD的面积为1,试用含m的代数式表示k.
,△OBD的面积为1,试用含m的代数式表示k.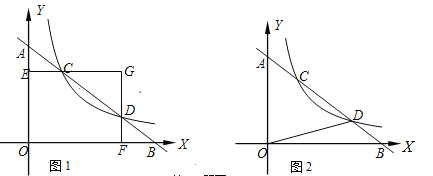
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB等于30°,角内有一点P,OP=6,点M在OA上,点N在OB上,△PMN周长的最小值是
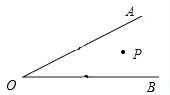
-
科目: 来源: 题型:
查看答案和解析>>【题目】每件a元的上衣先提价10%,再打九折以后出售的价格是 元/件;
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解居民用水情况,在某小区随机抽查了15户家庭的月用水量,结果如下表:
月用水量(吨)
4
5
6
8
9
户数
2
5
4
3
1
则这15户家庭的月用水量的众数与中位数分别为( )
A.9、6
B.6、6
C.5、6
D.5、5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为三角形ABD中线.
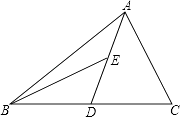
(1)在△BED中作BD边上的高EF;
(2)若△ABC的面积为40,BD=5,求EF的长.
相关试题

