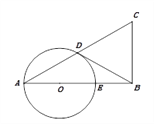
【题目】已知在△ABC中,∠ABC=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)求证: ![]() ;
;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
参考答案:
【答案】(1)证明见解析;(2)4.
【解析】试题分析:(1)本题利用两角法判定三角形相似,利用相似三角形的性质得出比例式即可;(2)利用切线的性质和特殊角的三角函数值判断出∠OBD=30°,进而得出∠BAC=30°,利用30°所对的直角边是斜边的一半即可得出.
试题解析:
(1)证明:连接DE,
∵AE是直径,∴∠ADE=90°.
∴∠ADE=∠ABC.
又∠A=∠A,∴△ADE∽△ABC. (3分)
∴![]() . (4分)
. (4分)
(2)解:连接OD,
∵BD是⊙O的切线,
∴OD⊥BD
∴∠ODB=90°. (5分)
∵在Rt△OBD中,E是OB的中点,
∴DE= ![]() =BE=OE=OD, (6分)
=BE=OE=OD, (6分)
∴sin∠OBD=![]() .
.
∴∠OBD=30° (7分)
同理∠BAC=30°. (8分)
在Rt△ABC中,AC=2BC=2×2=4.(9分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据3,4,10,7,6的中位数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
(1)请你判断OM与ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于E,当AB=5,AC=6时,求△BDE的周长.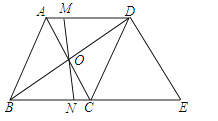
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 2a﹣a=1B. 2a+b=2ab
C. (a4)3=a7D. (﹣a)2(﹣a)3=﹣a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】“从布袋中取出一个红球的概率是0”这句话的意思就是取出一个红球的概率很小.以上理解是否正确?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:3﹣(﹣2)=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中,不能确定四边形ABCD为平行四边形的是( )
A. ∠A=∠C,∠B=∠D B. ∠A=∠B=∠C=90°
C. ∠A+∠B=180°,∠B+∠C=180° D. ∠A+∠B=180°,∠C+∠D=180°
相关试题

