【题目】平行四边形![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,若
,若![]() 、
、![]() 是
是![]() 上两动点,
上两动点,![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时以
两点同时以![]() 的相同的速度向
的相同的速度向![]() 、
、![]() 运动
运动

![]() 四边形
四边形![]() 是平行四边形吗?说明你的理由.
是平行四边形吗?说明你的理由.
![]() 若
若![]() ,
,![]() ,当运动时间
,当运动时间![]() 为多少时,以
为多少时,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为矩形.
为顶点的四边形为矩形.
参考答案:
【答案】(1)见解析;(2) t为2s时.
【解析】
(1)由平行四边形ABCD中,可得OA=OC,OB=OD,又由若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动,易得AE=CF,即可得OE=OF,则可判定四边形DEBF是平行四边形;
(2)由四边形DEBF是平行四边形,可得当EF=BD时,四边形DEBF为矩形,即可得方程:18-2t-2t=10,继而求得答案.
解:![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
理由:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∵![]() 、
、![]() 是
是![]() 上两动点,
上两动点,![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时以
两点同时以![]() 的相同的速度向
的相同的速度向![]() 、
、![]() 运动,
运动,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
![]() 根据题意得:
根据题意得:![]() 或
或![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴当![]() 时,四边形
时,四边形![]() 为矩形.
为矩形.
即![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
解得:![]() ,
,
∴当运动时间![]() 为
为![]() 时,四边形
时,四边形![]() 为矩形.
为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由.
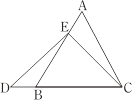
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,
中, 为对角线,
为对角线,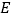 为
为 上一点,连接
上一点,连接 ,
, ,
, 的延长线交
的延长线交 于点
于点 ,
, ,则
,则 的度数为________.
的度数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中, ,
, ,点
,点 从
从 开始沿折线
开始沿折线 以
以 的速度运动,点
的速度运动,点 从
从 开始沿
开始沿 边以
边以 的速度移动,如果点
的速度移动,如果点 、
、 分别从
分别从 、
、 同时出发,当其中一点到达
同时出发,当其中一点到达 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为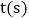 ,当
,当 ________时,四边形
________时,四边形 也为矩形.
也为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)
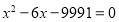 ; (2)
; (2)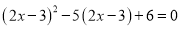 ;
;(3)
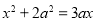 (配方法); (4)
(配方法); (4) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场礼品柜台元旦期间购进大量贺年卡,一种贺年卡平均每天可售出
 张,每张盈利
张,每张盈利 元.为了尽快减少库存,商场决定采取适当的降价措施,调查发现,如果这种贺年卡的售价每降低
元.为了尽快减少库存,商场决定采取适当的降价措施,调查发现,如果这种贺年卡的售价每降低 元,那么商场平均每天可多售出
元,那么商场平均每天可多售出 张.商场要想平均每天盈利
张.商场要想平均每天盈利 元,每张贺年卡应降价多少元?
元,每张贺年卡应降价多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】
 如图
如图 ,将直角的顶点
,将直角的顶点 放在正方形
放在正方形 的对角线
的对角线 上,使角的一边交
上,使角的一边交 于点
于点 ,另一边交
,另一边交 或其延长线于点
或其延长线于点 ,求证:
,求证: ;
; 如图
如图 ,将直角顶点
,将直角顶点 放在矩形
放在矩形 的对角线交点,
的对角线交点, 、
、 分别交
分别交 与
与 于点
于点 、
、 ,且
,且 平分
平分 .若
.若 ,
, ,求
,求 、
、 的长.
的长.
相关试题

