Question

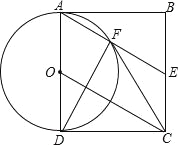
【题目】如图，四边形ABCD为矩形，E为BC边中点，以AD为直径的⊙O与AE交于点F．

（1）求证：四边形AOCE为平行四边形；

（2）求证：CF与⊙O相切；

（3）若F为AE的中点，求∠ADF的大小．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）30°．

【解析】

试题分析：（1）根据矩形的性质得到AD∥BC，AD=BC，∠ADC=90°，由E为BC边中点，AO=DO，得到AO=AD，EC=BC，等量代换得到AO=EC，AO∥EC，即可得到结论；

（2）利用平行四边形的判定方法得出四边形OAEC是平行四边形，进而得出△ODC≌△OFC（SAS），求出OF⊥CF，进而得出答案；

（3）如图，连接DE，由AD是直径，得到∠AFD=90°，根据点F为AE的中点，得到DF为AE的垂直平分线，根据线段垂直平分线的性质得到DE=AD，推出△ABE≌△DCE，根据全等三角形的性质得到AE=DE，推出三角形ADE为等边三角形，即可得到结论．

试题解析：（1）∵四边形ABCD是矩形，

∴AD∥BC，AD=BC，∠ADC=90°，

∵E为BC边中点，AO=DO，

∴AO=AD，EC=BC，

∴AO=EC，AO∥EC，

∴四边形OAEC是平行四边形；

（2）如图1，连接OF，

∵四边形OAEC是平行四边形

∴AE∥OC，

∴∠DOC=∠OAF，

∠FOC=∠OFA，

∵OA=OF，

∴∠OAF=∠OFA，

∴∠DOC=∠FOC，

在△ODC与△OFC中，

，

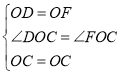∴△ODC≌△OFC（SAS），

∴∠OFC=∠ODC=90°，

∴OF⊥CF，

∴CF与⊙O相切；

（3）如图2，连接DE，

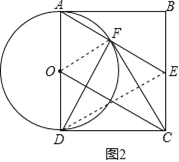
∵AD是直径，

∴∠AFD=90°，

∵点F为AE的中点，

∴DF为AE的垂直平分线，

∴DE=AD，

在△ABE与R△DCE中，

，

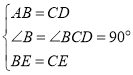∴△ABE≌△DCE，

∴AE=DE，

∴AE=DE=AD，

∴三角形ADE为等边三角形，

∴∠DAF=60°，

∴∠ADF=30°．