【题目】已知在长方形ABCD中,AB=4,BC= ![]() ,O为BC上一点,BO=
,O为BC上一点,BO= ![]() ,如图所示,以BC所在直线为x轴,O为坐标原点建立平面直角坐标系,M为线段OC上的一点.
,如图所示,以BC所在直线为x轴,O为坐标原点建立平面直角坐标系,M为线段OC上的一点.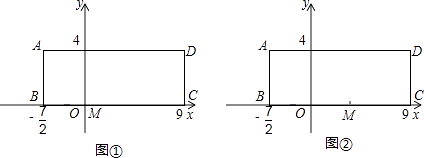
(1)若点M的坐标为(1,0),如图①,以OM为一边作等腰△OMP,使点P在y轴上,则符合条件的等腰三角形有几个?请直接写出所有符合条件的点P的坐标;
(2)若点M的坐标为(1,0),如图①,以OM为一边作等腰△OMP,使点P落在长方形ABCD的一边上,则符合条件的等腰三角形有几个?请直接写出所有符合条件的点P的坐标.
(3)若将(2)中的点M的坐标改为(4,0),其它条件不变,如图②,那么符合条件的等腰三角形有几个?求出所有符合条件的点P的坐标.
参考答案:
【答案】
(1)解:∵以OM为一边作等腰△OMP,点P在y轴上,
∴OP=OM,又点M的坐标为(1,0),
∴OP=OM=1,
∴符合条件的等腰三角形有2个,
则点P的坐标为(0,﹣1)、(0,1);
(2)解:由题意得,OM为等腰△OMP的底边,
则点P在线段OM的垂直平分线上,
∴点P的坐标为:(1,4),
则符合条件的等腰三角形有1个;
(3)解:如图,
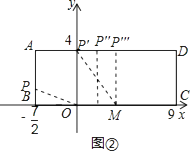
∵OP=OM,
∴OP=4,
∴BP= ![]() =
= ![]() ,
,
∴点P的坐标为(﹣ ![]() ,
, ![]() ),
),
由题意得,P′的坐标为(0,4),P′′的坐标为(1,4),P′′′的坐标为(4,4),
符合条件的等腰三角形有4个.
【解析】(1)抓住已知条件,是以OM为一边作等腰△OMP,且使点P在y轴上,根据等腰直角三角形的性质解答。
(2)根据线段垂直平分线的性质解答即可。
(3)分OM=OP、OP=PM、OM=MP三种情况,根据等腰三角形的性质解答.
【考点精析】掌握线段垂直平分线的性质和勾股定理的概念是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.某种物体的长度为0.0000000235m,用科学记数法表示为___________m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】第九届中国国际园林博览会(园博会)已于2013年5月18日在北京开幕,以下是根据近几届园博会的相关数据绘制的统计图的一部分:
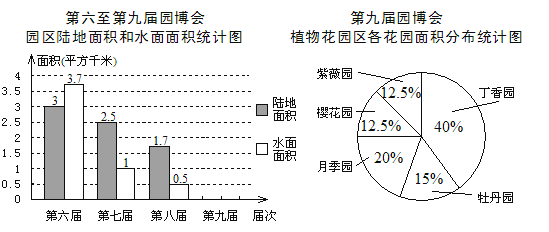
(1)第九届园博会的植物花园区由五个花园组成,其中月季园面积为0.04平方千米,牡丹园面积为 平方千米;
(2)第九届园博会园区陆地面积是植物花园区总面积的18倍,水面面积是第七、八两届园博会的水面面积之和,请根据上述信息补全条形统计图,并标明相应数据;
(3)小娜收集了几届园博会的相关信息(如下表),发现园博会园区周边设置的停车位数量与日接待游客量和单日最多接待游客量中的某个量近似成正比例关系,根据小娜的发现,请估计将于2015年举办的第十届园博会大约需要设置的停车位数量(直接写出结果,精确到百位)。
第七届至第十届园博会游客量与停车位数量统计表
日均接待游客量(万人次)
单日最多接待游客量(万人次)
停车位数量(个)
第七届
0.8
6
约3 000
第八届
2.3
8.2
约4 000
第九届
8(预计)
20(预计)
约10 500
第十届
1.9(预计)
7.4(预计)
约 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:
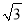 ,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).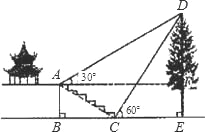
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b,函数值y随自变置x的增大而减小,且kb<0,则函数y=kx+b的图象大致是( )
A.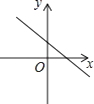
B.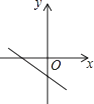
C.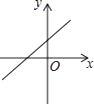
D.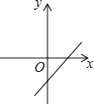
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=60°,∠B=2∠C,则∠B=_______ °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10
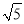 cm,且tan∠EFC=
cm,且tan∠EFC=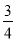 ,那么该矩形的周长为_____.
,那么该矩形的周长为_____.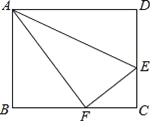
相关试题

