【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF. 
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
参考答案:
【答案】
(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°,
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF,
∴∠ABC﹣∠CBF=∠EBF﹣∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,有  ,
,
∴△ABF≌△CBE(SAS).

(2)解:△CEF是直角三角形.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°﹣∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB﹣∠FEB=135°﹣45°=90°,
∴△CEF是直角三角形.
【解析】(1)由四边形ABCD是正方形可得出AB=CB,∠ABC=90°,再由△EBF是等腰直角三角形可得出BE=BF,通过角的计算可得出∠ABF=∠CBE,利用全等三角形的判定定理SAS即可证出△ABF≌△CBE;(2)根据△EBF是等腰直角三角形可得出∠BFE=∠FEB,通过角的计算可得出∠AFB=135°,再根据全等三角形的性质可得出∠CEB=∠AFB=135°,通过角的计算即可得出∠CEF=90°,从而得出△CEF是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张买了张
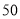 元的乘车IC卡,如果他乘车的次数用
元的乘车IC卡,如果他乘车的次数用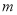 表示,则记录他每次乘车后的余额
表示,则记录他每次乘车后的余额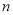 (元)如下表:
(元)如下表:次数m
余额n(元)
1
50—0.8
2
50—1.6
3
50—2.4
4
50—3.2
……
……
【1】⑴写出乘车的次数
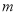 表示余额
表示余额 (元)的关系式;
(元)的关系式;【2】⑵利用上述关系式计算小张乘了13次车后还剩下多少元?
【3】⑶小张最多能乘几次车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,点M为锐角三角形ABC内任意一点,连接AM、BM、CM.以AB为一边向外作等边三角形△ABE,将BM绕点B逆时针旋转60°得到BN,连接EN.
(1)求证:△AMB≌△ENB;
(2)若AM+BM+CM的值最小,则称点M为△ABC的费马点.若点M为△ABC的费马点,试求此时∠AMB、∠BMC、∠CMA的度数;
(3)小翔受以上启发,得到一个作锐角三角形费马点的简便方法:如图②,分别以△ABC的AB、AC为一边向外作等边△ABE和等边△ACF,连接CE、BF,设交点为M,则点M即为△ABC的费马点.试说明这种作法的依据.
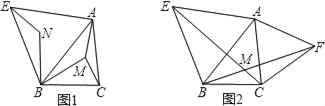
-
科目: 来源: 题型:
查看答案和解析>>【题目】2008年8月第29届奥运会将在北京开幕,5个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间2008年8月8日20时应是( )

A.伦敦时间2008年8月8日11时
B.巴黎时间2008年8月8日13时
C.纽约时间2008年8月8日5时
D.汉城时间2008年8月8日19时
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)当a≠0时,求
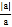 的值.(写出解答过程)
的值.(写出解答过程)(2)若a≠0,b≠0,且
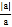 +
+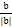 =0,则
=0,则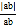 的值为 .
的值为 .(3)若ab>0,则
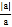 +
+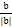 +
+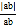 的值为 .
的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】为了贯彻落实健康第一的指导思想,促进学生全面发展,国家每年都要对中学生进行一次体能测试,测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级,某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析,并根据收集的数据绘制了两幅不完整的统计图,请根据这两幅统计图中的信息回答下列问题

(1)本次抽样调查共抽取多少名学生?
(2)补全条形统计图.
(3)在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.
(4)若该学校七年级共有600名学生,请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名?
(5)请你对“不及格”等级的同学提一个友善的建议(一句话即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AC⊥BD,AB=AD,要使四边形ABCD是菱形,只需添加一个条件,这个条件可以是_____(只要填写一种情况).
相关试题

