【题目】如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.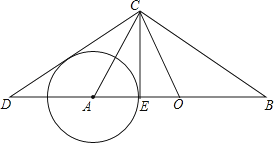
(1)求证:∠B=∠ACD.
(2)已知点E在AB上,且BC2=ABBE.
(i)若tan∠ACD= ![]() ,BC=10,求CE的长;
,BC=10,求CE的长;
(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
参考答案:
【答案】
(1)
证明:∵∠ACB=∠DCO=90°,
∴∠ACB﹣∠ACO=∠DCO﹣∠ACO,
即∠ACD=∠OCB,
又∵点O是AB的中点,
∴OC=OB,
∴∠OCB=∠B,
∴∠ACD=∠B
(2)
解:(i)∵BC2=ABBE,
∴ ![]() ,
,
∵∠B=∠B,
∴△ABC∽△CBE,
∴∠ACB=∠CEB=90°,
∵∠ACD=∠B,
∴tan∠ACD=tan∠B= ![]() ,
,
设BE=4x,CE=3x,
由勾股定理可知:BE2+CE2=BC2,
∴(4x)2+(3x)2=100,
∴解得x=2 ![]() ,
,
∴CE=6 ![]() ;
;
(ii)过点A作AF⊥CD于点F,
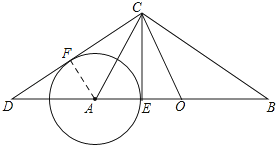
∵∠CEB=90°,
∴∠B+∠ECB=90°,
∵∠ACE+∠ECB=90°,
∴∠B=∠ACE,
∵∠ACD=∠B,
∴∠ACD=∠ACE,
∴CA平分∠DCE,
∵AF⊥CE,AE⊥CE,
∴AF=AE,
∴直线CD与⊙A相切
【解析】(1)因为∠ACB=∠DCO=90°,所以∠ACD=∠OCB,又因为点O是Rt△ACB中斜边AB的中点,所以OC=OB,所以∠OCB=∠B,利用等量代换可知∠ACD=∠B;(2)(i)因为BC2=ABBE,所以△ABC∽△CBE,所以∠ACB=∠CEB=90°,因为tan∠ACD=tan∠B,利用勾股定理即可求出CE的值;
(ii)过点A作AF⊥CD于点F,易证∠DCA=∠ACE,所以CA是∠DCE的平分线,所以AF=AE,所以直线CD与⊙A相切.本题考查圆的综合问题,涉及等量代换,勾股定理,相似三角形的判定与性质,锐角三角函数等知识,知识点较综合,需要学生灵活运用所学知识解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的
 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
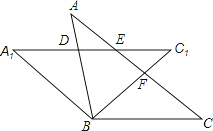
(1)求证:△BCF≌△BA1D.
(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,点D,E分别在AC,BC上,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若PF=3,则BP=( )
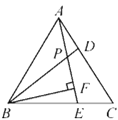
A. 6 B. 5 C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如图,线段AB=1=0﹣(﹣1);线段 BC=2=2﹣0;线段 AC=3=2﹣(﹣1)问题
①数轴上点M、N代表的数分别为﹣9和1,则线段MN= ;
②数轴上点E、F代表的数分别为﹣6和﹣3,则线段EF= ;
③数轴上的两个点之间的距离为5,其中一个点表示的数为2,则另一个点表示的数为m,求m.
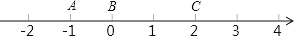
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,…每个正方形四条边上的整点的个数.按此规律推算出正方形A2 016B2 016C2 016D2 016四条边上的整点共有_________个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某月的日历表,在此日历表上可以用一个“十”字圈出5个数(如3,9,10,11,17).照此方法,若圈出的5个数中,最大数与最小数的和为46,则这5个数的和为( )
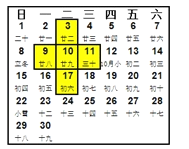
A. 205 B. 115 C. 85 D. 65
相关试题

