【题目】在△ABC中,P为边AB上一点.
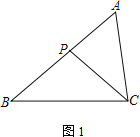
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
(2) 若M为CP的中点,AC=2,
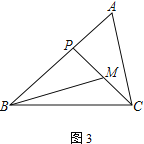
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.

参考答案:
【答案】(1)详见解析;(2)①BP=![]() ;②
;②![]() .
.
【解析】
试题分析:(1)根据已知条件易证△ACP∽△ABC,由相似三角形的性质即可证得结论;(2)①如图,作CQ∥BM交AB延长线于Q,设BP=x,则PQ=2x,易证△APC∽△ACQ,所以AC2=AP·AQ,由此列方程,解方程即可求得BP的长;②如图:作CQ⊥AB于点Q,作CP0=CP交AB于点P0,再证△AP0C∽△MPB,(2)的方法求得AP0的长,即可得BP的长.
试题解析:(1)证明:∵∠ACP=∠B,∠BAC=∠CAP,
∴△ACP∽△ABC,
∴AC:AB=AP:AC,
∴AC2=AP·AB;
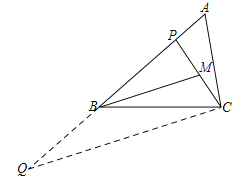
(2)①如图,作CQ∥BM交AB延长线于Q,设BP=x,则PQ=2x
∵∠PBM=∠ACP,∠PAC=∠CAQ,
∴△APC∽△ACQ,
由AC2=AP·AQ得:22=(3-x)(3+x),∴x=![]()
即BP=![]() ;
;
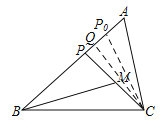
②如图:作CQ⊥AB于点Q,作CP0=CP交AB于点P0,
∵AC=2,∴AQ=1,CQ=BQ=![]() ,
,
设AP0=x,P0Q=PQ=1-x,BP=![]() -1+x,
-1+x,
∵∠BPM=∠CP0A,∠BMP=∠CAP0,
∴△AP0C∽△MPB,∴![]() ,
,
∴MP P0C=![]() AP0 BP=x(
AP0 BP=x(![]() -1+x),
-1+x),
解得x=![]()
∴BP=![]() -1+
-1+![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,其逆命题成立的是__.(只填写序号)
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在跳远测试中,甲同学超过达标线20cm,我们记为+20,乙同学还差10cm达标,应记为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】公园中儿童游乐场是两个相似三角形地块,相似比为2:3,其中大三角形地块面积为27,则小三角形地块的面积是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:≈1.73,≈1.41.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a5·a3正确的是( )
A. a2 B. a8 C. a10 D. a15
-
科目: 来源: 题型:
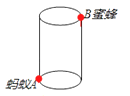
查看答案和解析>>【题目】如图,圆柱形容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外壁底部与蜂蜜相对的A处,
(1)求蚂蚁从A到B处吃到蜂蜜最短距离;
(2)若蚂蚁刚出发时发现B处的蜂蜜正以每秒钟1cm沿杯内壁下滑,4秒钟后蚂蚁吃到了蜂蜜,求蚂蚁的平均速度至少是多少?
相关试题

