搜索
【题目】已知关于x的一元二次方程x2＋(2k－1)x＋k2＋1＝0，如果方程的两根之和等于两根之积，求k的值．
参考答案：
【答案】k＝－2.
【解析】
设方程的两根为x1，x2，根据根的判别式得到△=（2k-1）2-4（k2+1）≥0，解得k≤-
，根据根与系数的关系得到x1+x2=-（2k-1）=1-2k，x1x2=k2+1，则1-2k=k2+1，可解得k1=0，k2=-2，然后根据k的取值范围可确定满足条件的k的值．
设方程的两根为x1，x2，
根据题意得△=（2k-1）2-4（k2+1）≥0，解得k≤-，
x1+x2=-（2k-1）=1-2k，x1x2=k2+1，
∵方程的两根之和等于两根之积，
∴1-2k=k2+1
∴k2+2k=0，
∴k1=0，k2=-2，
而k≤-，
∴k=-2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解方程：(1)
； （2）
.【答案】（1）x1 =1 ，x2=
； (2) x1 =-1，x2=
.【解析】试题分析：
根据两方程的特点，使用“因式分解法”解两方程即可.
试题解析：
（1）原方程可化为：
，方程左边分解因式得：
，
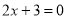或
，解得：
， 
.（2）原方程可化为：
，即
，∴
，∴
或
，解得：
.【题型】解答题
【结束】
20【题目】已知x1，x2是关于x的一元二次方程x2－2(m＋1)x＋m2＋5＝0的两实根．
(1)若(x1－1)(x2－1)＝28，求m的值；
(2)已知等腰△ABC的一边长为7，若x1，x2恰好是△ABC另外两边的边长，求这个三角形的周长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在求1+2+22+23+24+25+26的值时，小明发现：从第二个加数起每一个加数都是前一个加数的2倍，于是他设：S=1+2+22+23+24+25+26 为①式，然后在①式的两边都乘以2，得：2S=2+22+23+24+25+26+27 为②式；②﹣ ①得2S﹣S=27﹣1，S=27﹣1，即1+2+22+23+24+25+26=27﹣1．
（1）求1+3+32+33+34+35+36的值；
（2）求1+a+a2+a3+…+a2016（a≠0且a≠1）的值．
-
科目： 来源： 题型：
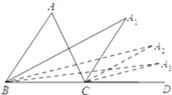
查看答案和解析>>【题目】如图，BA1和CA1分别是△ABC的内角平分线和外角平分线， BA2是∠A1BD的角平分线，CA2 是∠A1CD的角平分线，BA3是∠A2BD的角平分线，CA3 是∠A2CD的角平分线，若∠A＝ α，则∠A2019＝______________.
-
科目： 来源： 题型：
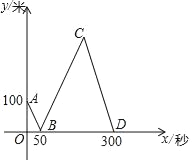
查看答案和解析>>【题目】甲、乙两人骑自行车匀速同向行驶，乙在甲前面100米处，同时出发去距离甲1300米的目的地，其中甲的速度比乙的速度快．设甲、乙之间的距离为y米，乙行驶的时间为x秒，y与x之间的关系如图所示．甲到达目的地时，乙距目的地还有_____米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“万州古红桔”原名“万县红桔”，古称丹桔（以下简称为红桔），种植距今至少已有一千多年的历史，“玫瑰香橙”（源自意大利西西里岛塔罗科血橙，以下简称香橙）现已是万州柑橘发展的主推品种之一．某水果店老板在2017年11月份用15200元购进了400千克红桔和600千克香橙，已知香橙的每千克进价比红桔的每千克进价2倍还多4元．
（1）求11月份这两种水果的进价分别为每千克多少元？
（2）时下正值柑橘销售旺季，水果店老板决定在12月份继续购进这两种水果，但进入12月份，由于柑橘的大量上市，红桔和香橙的进价都有大幅下滑，红桔每千克的进价在11月份的基础上下降了
m%，香橙每千克的进价在11月份的基础上下降了m%，由于红桔和“玫瑰香橙”都深受库区人民欢迎，实际水果店老板在12月份购进的红桔数量比11月份增加了
m%，香橙购进的数量比11月份增加了2m%，结果12月份所购进的这两种柑橘的总价与11月份所购进的这两种柑橘的总价相同，求m的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知 AD 是△ABC 的边 BC 上的中线．
（1）作出△ABD 的边 BD 上的高．
（2）若△ABC 的面积为 10，求△ADC 的面积．
（3）若△ABD 的面积为 6，且 BD 边上的高为 3，求 BC 的长．
相关试题
