【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)则样本容量容量是______________,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率。

参考答案:
【答案】(1)、50;图形见解析;(2)、90;(3)、![]() .
.
【解析】
试题分析:(1)、根据题意得出B的百分比,然后得出人数,根据C的百分比得出C组别的人数,然后进行补全;(2)、首先求出不少于12的频率,然后进行计算;(3)、根据题意画出树状图,然后得出概率.
试题解析:(1)、根据题意得:B:8%=5:2 则B=20% 10÷20%=50
C组别的人数:50×30%=15(人)
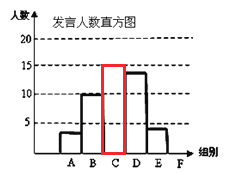
(2)、∵在统计的50人中,发言次数大于12的有4+5=9人,∴在这天里发言次数不少于12的频率为9÷50=18%。∴全年级500人中,在这天里发言次数不少于12的次数为500×18%=90(次)。
(3)、∵A组发言的学生为3人,∴有1位女生,2位男生。∵E组发言的学生: 4人,
∴有2位女生,2位男生。∴由题意可画树状图为:
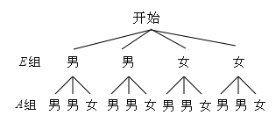
∴共有12种情况,所抽的两位学生恰好是一男一女的情况有6种,∴所抽的两位学生恰好是一男一女的概率为![]() =
=![]() 。
。
-
科目: 来源: 题型:
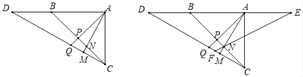
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,∠ABC=45°,点D为AB延长线上一点,连接CD,∠AMC=90°,AM交BC于点N,∠APB=90°,AP交CD于点Q.
(1)求证:AN=CQ;
(2)如图,点E在BA的延长线上,且AD=BE,连接EN并延长交CD于点F,求证:DQ=EN;
(3)在(2)的条件下,当3AE=2AB时,请直接写出EN:FN的值为 .
-
科目: 来源: 题型:
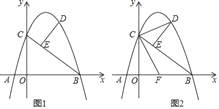
查看答案和解析>>【题目】如图,A(﹣1,0),B(4,0),C(0,3)三点在抛物线y=ax2+bx+c上,D为直线BC上方抛物线上一动点,E在CB上,∠DEC=90°
(1)求抛物线的函数表达式;
(2)如图1,求线段DE长度的最大值;
(3)如图2,F为AB的中点,连接CF,CD,当△CDE中有一个角与∠CFO相等时,求点D的横坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是( )

A. 8B. 10C. 10.4D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形,请你一一列举;
(2)求证:CF=EF.

-
科目: 来源: 题型:
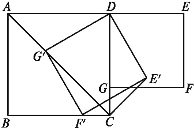
查看答案和解析>>【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE'F'G',此时点G'在AC上,连接CE',则CE'+CG'=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知顶点为P的抛物线C1的解析式为y=a(x-3)2(a≠0),且经过点(0,1).
(1)求a的值及抛物线C1的解析式;
(2)如图,将抛物线C1向下平移h(h>0)个单位得到抛物线C2,过点K(0,m2)(m>0)作直线l平行于x轴,与两抛物线从左到右分别相交于A,B,C,D四点,且A,C两点关于y轴对称.
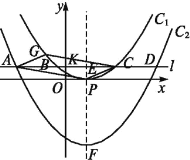
①点G在抛物线C1上,当m为何值时,四边形APCG为平行四边形?
②若抛物线C1的对称轴与直线l交于点E,与抛物线C2交于点F.试探究:在K点运动过程中,
 的值是否改变?若会,请说明理由;若不会,请求出这个值.
的值是否改变?若会,请说明理由;若不会,请求出这个值.
相关试题

