搜索
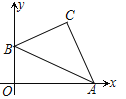
【题目】在平面直角坐标系中，已知点A、B的坐标分别为
A（6，0）、B（0，2），以AB为斜边在右上方作Rt△ABC.设点C坐标为（x，y），则（x+y）的最大值为__．
参考答案：
【答案】4+2
【解析】如图所示，
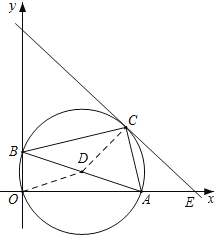
根据以AB为斜边在右上方作RtABC，可知点C在以AB为直径的⊙D上运动，根据点C坐标为（x，y）可构造新的函数x+y=m，则函数与y轴交点最高处即为x+y的最大值，此时，直线y=-x+m与⊙D相切，再根据圆心点的坐标，可得C的坐标，为（3+
，1+
），代入直线y=-x+m，可得4+2
，即可得出x+y的最大值为4+2
.
“点睛”本题主要考查了切线的性质，待定系数法求一次函数解析式以及等腰三角形的性质的综合应用，解决问题的关键是构造一次函数图象，根据圆的切线垂直于经过切点的半价进行求解.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若3×9m×27m=321 ， 则m的值为（ ）
A.3
B.4
C.5
D.6 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，分别以点A和点B为圆心，大于
AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．若△ADC的周长为10，AB=7，则△ABC的周长为（ ）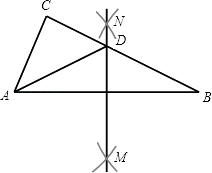 
A.7
B.14
C.17
D.20 -
科目： 来源： 题型：
查看答案和解析>>【题目】2▽4=8，5▽3=13，3▽5=11，9▽7=25。以此类推，计算：7▽3。
-
科目： 来源： 题型：
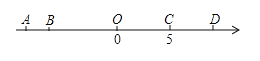
查看答案和解析>>【题目】如图，数轴上有A、B、C、D、O五个点，点O为原点，点C在数轴上表示的数是5，线段CD的长度为4个单位，线段AB的长度为2个单位，且B、C两点之间的距离为11个单位，请解答下列问题：
（1）点D在数轴上表示的数是 ，点A在数轴上表示的数是 ；
（2）若点B以每秒2个单位的速度向右匀速运动t秒运动到线段CD上，且BC的长度是3个单位，根据题意列出的方程是 ，解得t= ；
（3）若线段AB、CD同时从原来的位置出发，线段AB以每秒2个单位的速度向右匀速运动，线段CD以每秒3个单位的速度向左匀速运动，把线段CD的中点记作P，请直接写出，点P与线段AB的一个端点的距离为1.5个单位时运动的时间．
-
科目： 来源： 题型：
查看答案和解析>>【题目】请从以下两个小题中任选一个作答，若多选，则按第一题计分．
A．一个八边形的外角和是___度．
B．计划在楼层间修建一个坡角为35°的楼梯，若楼层间高度为2.7m，为了节省成本，现要将楼梯坡角增加11°，则楼梯的斜面长度约减少__m．（用科学计算器计算，结果精确到0.01m）
-
科目： 来源： 题型：
查看答案和解析>>【题目】⊙表示一种新运算符号。已知2⊙3=9，7⊙2=15，3⊙5=25。按此规律计算：16⊙4。
相关试题
