【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D. 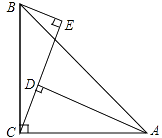
(1)求证:△ADC≌△CEB.
(2)AD=6cm,DE=4cm,求BE的长度.
参考答案:
【答案】
(1)证明:∵∠ACB=90°,BE⊥CE,AD⊥CE,
∴∠E=∠ADC=∠ACB=90°,
∴∠BCE+∠ACD=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中
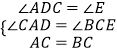
∴△ADC≌△CEB(AAS)
(2)解:∵△ADC≌△CEB,AD=6cm,
∴CE=AD=6cm,BE=CD,
∵DE=4cm,
∴BE=CD=CE﹣DE=6cm﹣4cm=2cm.
【解析】(1)求出∠E=∠ADC=∠ACB=90°,∠CAD=∠BCE,根据AAS推出即可;(2)根据全等三角形的性质求出CE=AD=6cm,BE=CD,即可得出答案.
【考点精析】通过灵活运用等腰直角三角形,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AC=BC,∠ACB=90°,点D为AC的中点.
(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,过点F作FH⊥FC,交直线AB于点H.判断FH与FC的数量关系并加以证明;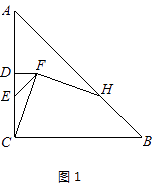
(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.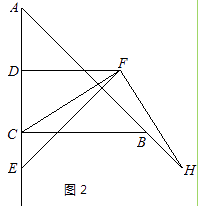
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中是真命题的是( )
A. <span style="color: rgb(169, 68, 66); font-size: 12px; line-height: 17.1429px; background-color: rgb(245, 245, 245);">经过直线外一点,有且只有一条直线与已知直线垂直</span>
B. 平分弦的直径垂直于弦。
C. 对角线互相平分且垂直的四边形是菱形 。
D. 反比例函数
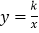 ,当k<0时,y随x的增大而增大。
,当k<0时,y随x的增大而增大。 -
科目: 来源: 题型:
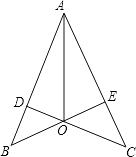
查看答案和解析>>【题目】如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,且AO平分∠BAC,那么图中全等三角形共有( )对.
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】有理数3.645精确到百分位的近似数为( )
A.3.6
B.3.64
C.3.7
D.3.65 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=3x2的开口方向是( )
A.向上
B.向下
C.向左
D.向右 -
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形B,C,E在同一条直线上,连结DC.
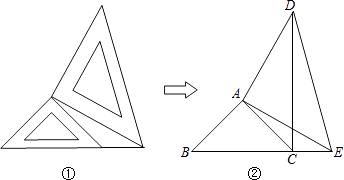
(1)请找出图②中的全等三角形,并给予说明(注意:结论中不得含有未标识的字母);
(2)请判断DC与BE的位置关系,并证明;
(3)若CE=2,BC=4,求△DCE的面积.
相关试题

